Action Principle (Classical)

In the context of modern physics development, consider a functional integral problem: $$ S[F(x, \dot{x}, t)] = \int_a^b F(x, \dot{x}, t) \, dt $$ where \( x = x(t) \) and \( \dot{x} = \frac{dx}{dt} \). If we change the trajectory \( x(t) \) while keeping \( a \) and \( b \) fixed, it affects the integral \( S \). We want to find the form of \( x(t) \) or the conditions that \( F(x, \dot{x}, t) \) must satisfy for \( S \) to have an extremum (whether maximum or minimum). According to the concept of calculus, if \( f(x) \) is at an extremum \( x_0 \), a small change \( x_0 + \varepsilon \) will not change \( f(x) \), i.e., \( df = 0 \). Similarly, for \( S \) to be at an extremum, a small change in \( x(t) \) results in \( \delta S = 0 \). We can represent the integral problem graphically; different functions \( x(t) \) represent different paths connecting points \( a \) and \( b \).

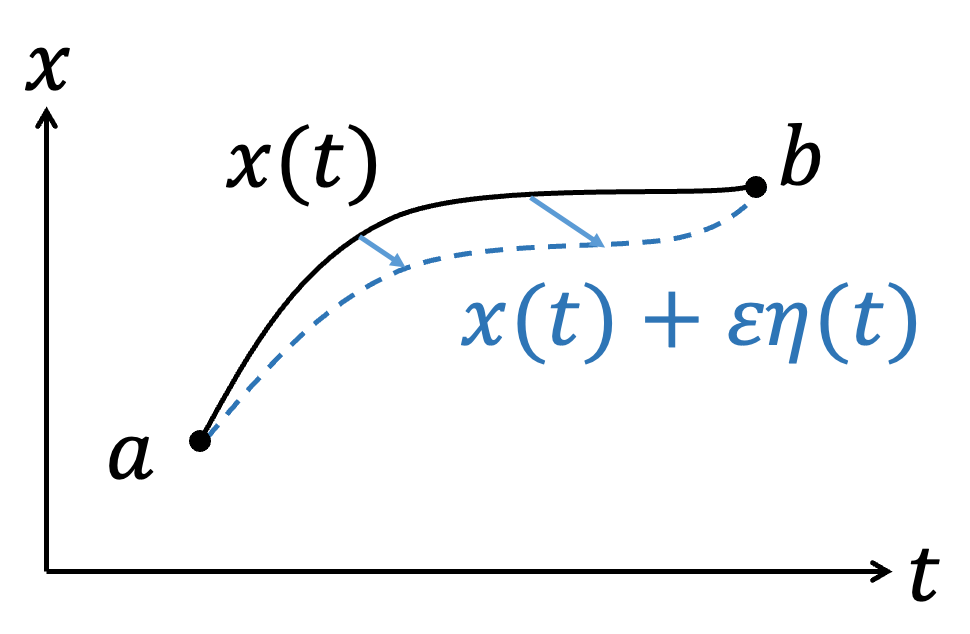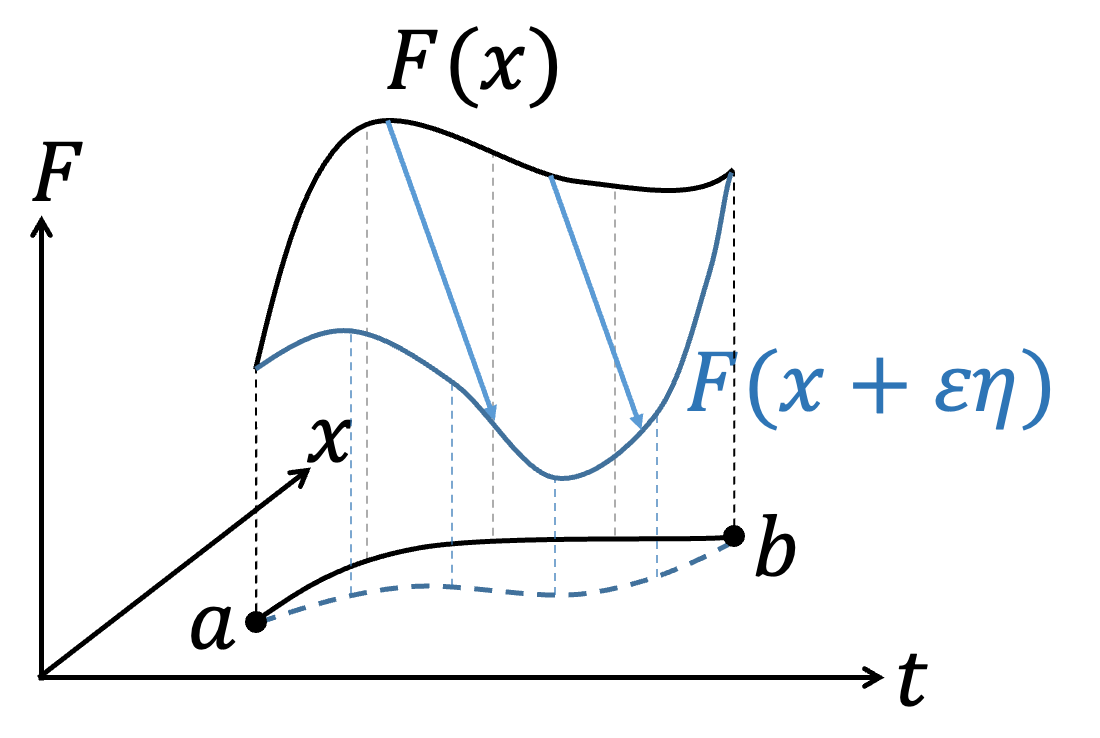If \( x(t) \) satisfies the extremum condition for \( S \), then adding a small arbitrary function \( \varepsilon \eta(t) \) (where \( \eta(a) = \eta(b) = 0 \)) will not change \( F(x, \dot{x}, t) \) at points \( a \) and \( b \). After adding this small arbitrary function \( \varepsilon \eta(t) \), we get: $$ x(t) \rightarrow x(t) + \varepsilon \eta(t) $$ $$ \dot{x}(t) \rightarrow \dot{x}(t) + \varepsilon \dot{\eta}(t) $$ $$ F(x, \dot{x}, t) \rightarrow F(x + \varepsilon \eta, \dot{x} + \varepsilon \dot{\eta}, t) = F(x, \dot{x}, t) + \delta F $$ We know that \( S \) remains unchanged for small variations \( \varepsilon \) near the extremum: $$ \delta S = S[F(x + \varepsilon \eta, \dot{x} + \varepsilon \dot{\eta}, t)] - S[F(x, \dot{x}, t)] = 0 \leftrightarrow \frac{\delta S}{\delta \varepsilon} = 0 $$ The change in \( \delta S \) is entirely due to \( \delta F \), so we can write: $$ \frac{\delta S}{\delta \varepsilon} = \frac{\delta}{\delta \varepsilon} \int_a^b F \, dt = \int_a^b \frac{\delta F}{\delta \varepsilon} \, dt = 0 $$ Using calculus, we expand \( \frac{\delta F}{\delta \varepsilon} \): $$ \frac{\delta S}{\delta \varepsilon} = \int_a^b \frac{\delta F}{\delta \varepsilon} \, dt = \int_a^b \left( \frac{\partial F}{\partial x} \frac{\delta x}{\delta \varepsilon} + \frac{\partial F}{\partial \dot{x}} \frac{\delta \dot{x}}{\delta \varepsilon} + \frac{\partial F}{\partial t} \frac{\delta t}{\delta \varepsilon} \right) dt $$ However, since we only vary the trajectory \( \eta \) and not \( t \), we have: $$ \frac{\delta t}{\delta \varepsilon} = 0 $$ Thus: $$ \frac{\delta S}{\delta \varepsilon} = \int_a^b \left( \frac{\partial F}{\partial x} \frac{\delta x}{\delta \varepsilon} + \frac{\partial F}{\partial \dot{x}} \frac{\delta \dot{x}}{\delta \varepsilon} \right) dt $$ Observing \( \frac{\delta x}{\delta \varepsilon} \) and \( \frac{\delta \dot{x}}{\delta \varepsilon} \): $$ \frac{\delta x}{\delta \varepsilon} = \frac{\delta}{\delta \varepsilon} (x + \varepsilon \eta) = \eta $$ $$ \frac{\delta \dot{x}}{\delta \varepsilon} = \frac{\delta}{\delta \varepsilon} (\dot{x} + \varepsilon \dot{\eta}) = \dot{\eta} $$ We get: $$ \frac{\delta S}{\delta \varepsilon} = \int_a^b \left( \frac{\partial F}{\partial x} \eta + \frac{\partial F}{\partial \dot{x}} \dot{\eta} \right) dt $$ $$ = \int_a^b \frac{\partial F}{\partial x} \eta \, dt + \int_a^b \frac{\partial F}{\partial \dot{x}} \frac{d \eta}{dt} \, dt $$ We perform integration by parts on the last term: $$\int_a^b {\partial F\over\partial \dot{x} } {d\eta \over dt} dt={\color{red}{{ \partial F\over\partial \dot{x} }\eta\Big|_a^b}}-\int_a^b {d\over dt}{\partial F\over\partial \dot{x}}\eta dt$$ Note the term in red: Since \( \eta(t) \) satisfies \( \eta(a) = \eta(b) = 0 \), we have \(\color{red}{{ \partial F\over\partial \dot{x} }\eta\Big|_a^b=0}\): $$ \therefore \frac{\delta S}{\delta \varepsilon} = \int_a^b \frac{\partial F}{\partial x} \eta \, dt - \int_a^b \frac{d}{dt} \left( \frac{\partial F}{\partial \dot{x}} \right) \eta \, dt $$ $$ = \int_a^b \left( \frac{\partial F}{\partial x} - \frac{d}{dt} \left( \frac{\partial F}{\partial \dot{x}} \right) \right) \eta \, dt = 0 $$ Since \( \eta(t) \) is arbitrary, we have: $$ \frac{\partial F}{\partial x} - \frac{d}{dt} \left( \frac{\partial F}{\partial \dot{x}} \right) = 0 $$ This is the Euler-Lagrange equation.

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.