Critical Coupling Constants

DOI:10.1038/s41598-023-33809-5

My Ph.D. thesis is “The effect of critical coupling constants on superconductivity enhancement”. In the thesis, it clearly elaborated that the superconducting dome appears when the coupling strength approached to the critical coupling constants. Varying the phonon spectrum \(\Omega\), tuning the carrier number \(𝑍\), and increasing the pressure \(𝑃\) were three important approaches to enhance superconductivity \(𝑇_𝑐\). I extended the BCS-McMillan theory to unify effects of the phonon frequency \(\Omega\), the carrier number \(𝑍\), and the pressure \(𝑃\) on superconductivity.

Quantum Hamiltonian of Superconductivity

The quantum Hamiltonian of superconductivity is: $$\hat{H} \left| \Psi \right> =\left[ \sum\limits_{k\sigma} \xi_k \hat{c}_{k\sigma}^\dagger \hat{c}_{k\sigma} + \frac{1}{N}\sum\limits_{kk^\prime} \frac{g_{eff}}{M\Omega^2} \hat{c}_{k\uparrow}^\dagger \hat{c}_{k\downarrow}^\dagger \hat{c}_{-k^\prime \downarrow} \hat{c}_{k^\prime \uparrow} \right] \left| \Psi \right>$$ I derived the explicit form of coupling constant \(\lambda\) and \(𝑇_𝑐\) are $$\lambda = { C \sqrt[3]{Zn_{ion}}\over M\Omega ^2} $$ and $$T_c \sim \Omega\cdot exp\left(-{1 \over \lambda}\right) = \Omega\cdot exp\left[-{M\Omega ^2 \over C \sqrt[3]{Zn_{ion}}}\right]$$ , where \(C\) is a constant, \(M\) is the ion mass, \(Z\) is the valence number, and \(n_{ion}\) is the ion number density. The derivative of \(𝑇_𝑐\) with respect to \(\Omega\) is $${dT_c \over d\Omega}\sim {T_c \over \Omega}\cdot \left[1-{2\over \lambda}\right]$$ The derivative \(dT_c\over d\Omega\) is equal to 0 when \(\lambda\) is equal to 2. Define the critical coupling constant corresponding to the phonon frequency \(\lambda_c^\Omega=2\). Similarly, one can derived other two critical coupling constants \(\lambda_c^Z= {5 \over 3}\), and \(\lambda_c^P={4 \over 3}\).

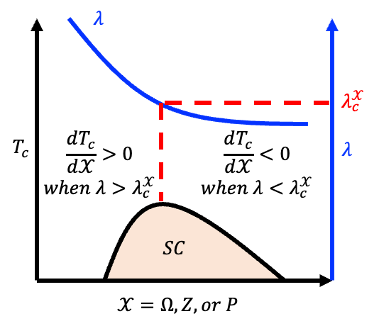
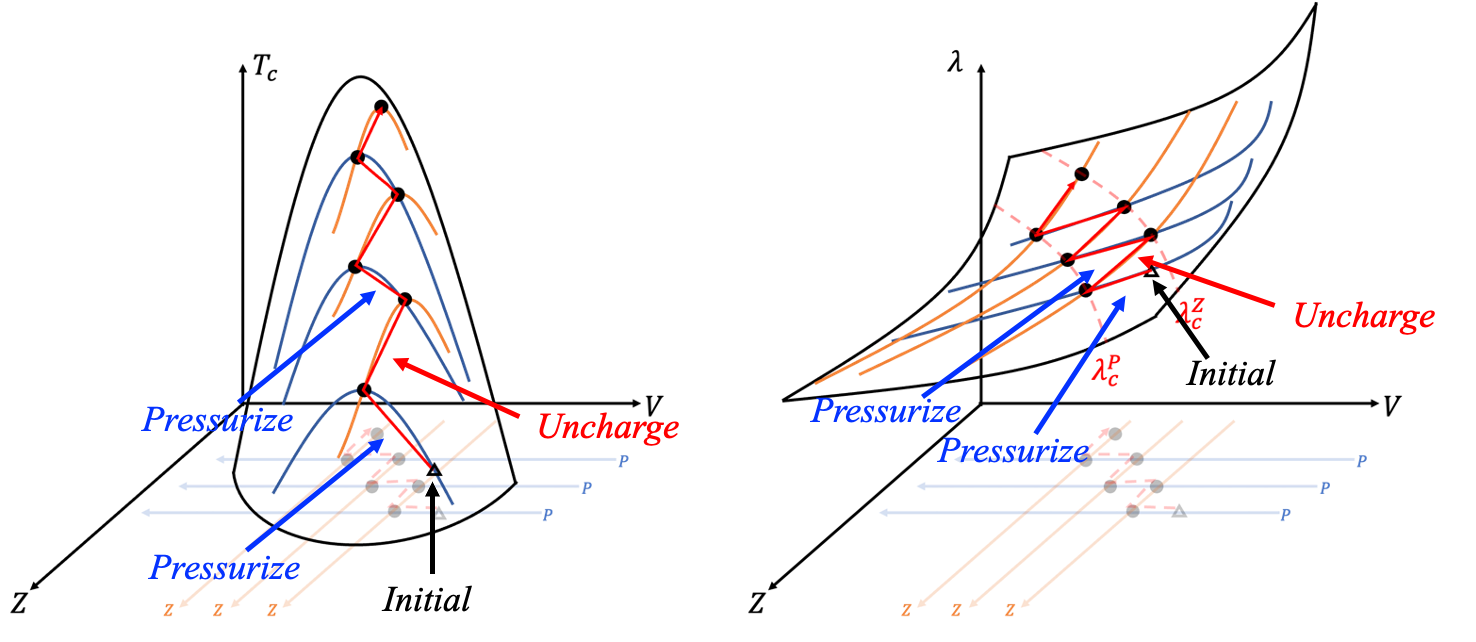
These critical coupling constants are consistent with experimental observations and quantitatively classify superconductivity into three categories: weak (\(\lambda_c < \lambda_c^P\)) , intermediate (\(\lambda_c^P < \lambda_c^\Omega\)) , and strong coupling (\(\lambda_c > \lambda_c^\Omega\)) . Each category corresponds to different enhancement strategies. More precisely, the enhancement strategies for weak and strong coupling regions are opposite, but both inevitably bring superconductivity into the intermediate coupling region. For superconductors in the intermediate coupling region, general zigzag strategies further enhance the superconductivity. In particular, take that \(\lambda\) belongs in the interval \(\lambda_c^P<\lambda<\lambda_c^Z\) for the following discussion without loss of generality. In this interval, superconductivity can be enhanced by increasing \(P\) or decreasing \(Z\). First, let the superconductivity be optimized by tuning \(Z\), such that \(\lambda\) is equal to \(\lambda_c^Z\), denoted as \(\lambda_1\). Second, since \(\lambda_1\) is larger than \(\lambda_c^P\), we can increase \(P\) to increase \(T_c\). The second step causes \(\lambda\) to decrease and \(T_c\) is optimized when \(\lambda=\lambda_c^P\), denoted as \(\lambda_2\). Third, now \(\lambda_2\) is smaller than \(\lambda_c^Z\), \(T_c\) can be further increased by decreasing \(Z\). The third step increases \(\lambda\) and \(T_c\) is optimized when \(\lambda=\lambda_c^Z\), denoted as \(\lambda_3\). Repeat step 2 and step 3 by increasing \(P\) and decreasing \(Z\) alternately; \(T_c\) can be enhanced like a zigzag mountain climbing.

(Click to enlarge)

According to the theory, I focused on the chemical design including high phonon frequency, multiple carriers, and small lattice constants. I synthesized a series of high-entropy oxides (HEO) based on \(Bi_2Sr_2Ca_2Cu_3O_x\) and \(YBa_2Cu_3O_x\) superconductors. The micro structure of the HEO compounds was analyzed by ZEISS Gemini SEM and Bruker D2 PHASER XRD.

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.