Action Principle (Classical)

In the previous section, we introduced the basic concept of the variational method, but it required introducing an arbitrary function \(\eta(t)\), which made the process somewhat cumbersome and less conducive to further operations. In this section, we will demonstrate the variational method using the same concept but with a more abstract approach and similar mathematical techniques. This approach is somewhat analogous to treating the variational operation similarly to differentiation.

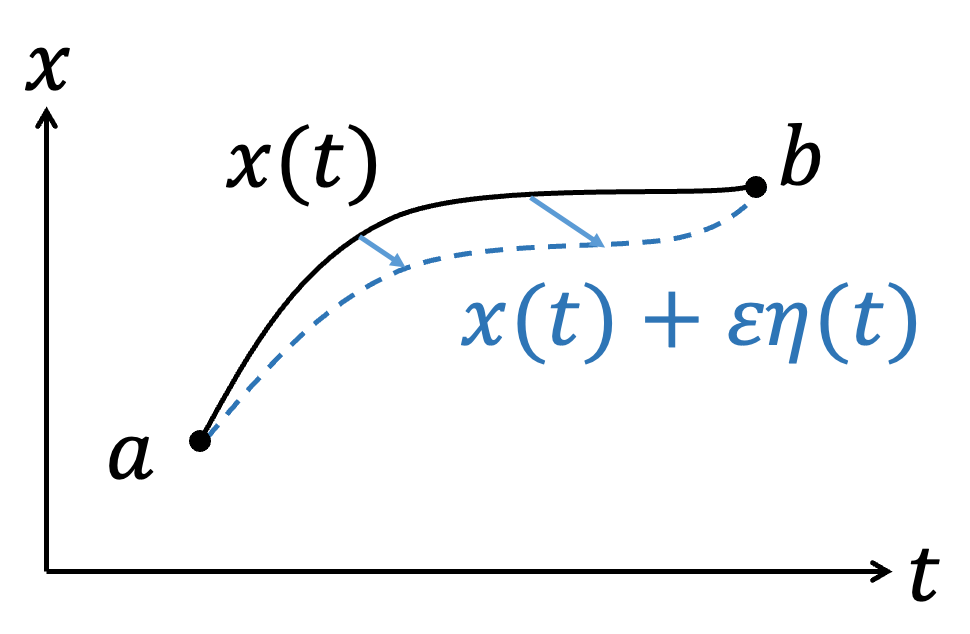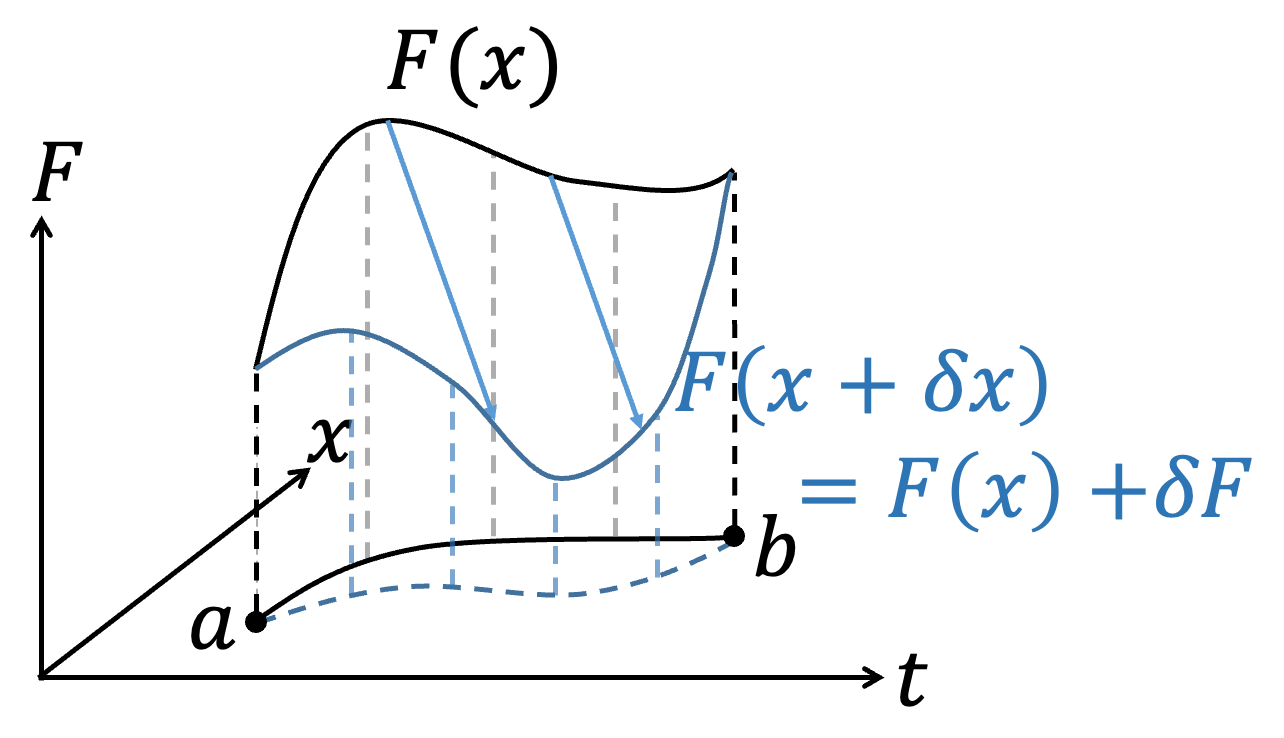For the same integral problem involving a functional: $$S[F(x,\dot{x},t)] = \int_a^b F(x,\dot{x},t)\, dt$$ When we perform a variation with respect to \(x\): $$x \to x + \delta x$$ The variation \(\delta x\) satisfies: $$\delta x(a) = \delta x(b) = 0$$ The variation in \(x\) will lead to changes in \(\dot{x}\) and \(F\): $$ \dot{x}(x) \to \dot{x}(x + \delta x) = \dot{x}(x) + \delta \dot{x}$$ $$F(x,\dot{x},t) \to F(x + \delta x, \dot{x}(x) + \delta \dot{x}, t) = F(x,\dot{x},t) + \delta F$$ We require \(\delta S = 0\): $$\delta S = \delta \int_a^b F\, dt = \int_a^b \delta F\, dt = 0$$ Conceptually, it is easy to understand that the variation \(\delta F\) is related to \(\delta x\) and \(\delta \dot{x}\), so expanding \(\delta F\), we get: $$\delta S = \int_a^b \delta F\, dt = \int_a^b \left( \frac{\partial F}{\partial x} \delta x + \frac{\partial F}{\partial \dot{x}} \delta \dot{x} \right)\, dt$$

Advanced: Thm. 1: Interchangeability of Differentiation and Variation If differentiation and variation are applied to different objects, such as differentiation with respect to \(t\), \( \frac{d}{dt} \) and variation with respect to \(x\), \left(\frac{\partial q}{\partial s}\right) d\dot{s} \(\delta x\), then \( \frac{d}{dt} \) and \( \delta \) can be interchanged. $$\delta \dot{f} = \dot{f}(x + \delta x) - \dot{f}(x)$$ $$= \frac{d}{dt} \left( f(x + \delta x) - f(x) \right) = \frac{d}{dt} \delta f$$

Interchanging \(\delta \dot{x}\) with \(\frac{d}{dt} \delta x\): $$\delta S = \int_a^b \frac{\partial F}{\partial x} \delta x\, dt + \int_a^b \frac{\partial F}{\partial \dot{x}} \left( \frac{d}{dt} \delta x \right)\, dt$$ Using the same method, we perform integration by parts on the second term: $$\int_a^b \frac{\partial F}{\partial \dot{x}} \left( \frac{d}{dt} \delta x \right)\, dt = \color{red}{\frac{\partial F}{\partial \dot{x}} \delta x \Big|_a^b} - \int_a^b \frac{d}{dt} \frac{\partial F}{\partial \dot{x}} \delta x\, dt$$ Note the red term: since we require the variation \(\delta x\) to satisfy \(\delta x(a) = \delta x(b) = 0\), we have \(\color{red}{\frac{\partial F}{\partial \dot{x}} \delta x \Big|_a^b = 0}\). $$\delta S = \int_a^b \frac{\partial F}{\partial x} \delta x\, dt - \int_a^b \left( \frac{d}{dt} \frac{\partial F}{\partial \dot{x}} \right) \delta x\, dt$$ $$= \int_a^b \left( \frac{\partial F}{\partial x} - \frac{d}{dt} \frac{\partial F}{\partial \dot{x}} \right) \delta x\, dt = 0$$ \(\delta x\) is arbitrary. $$ \frac{\partial F}{\partial x} - \frac{d}{dt} \frac{\partial F}{\partial \dot{x}} = 0$$ This is the Euler-Lagrange equation.

Advanced: Thm. 2: Chain Rule for Variation $$\delta (FG) = \frac{\partial (FG)}{\partial x} \delta x + \frac{\partial (FG)}{\partial \dot{x}} \delta \dot{x}$$ $$= \left( \frac{\partial F}{\partial x} G + F \frac{\partial G}{\partial x} \right) \delta x + \left( \frac{\partial F}{\partial \dot{x}} G + F \frac{\partial G}{\partial \dot{x}} \right) \delta \dot{x}$$ $$= \left( \frac{\partial F}{\partial x} \delta x + \frac{\partial F}{\partial \dot{x}} \delta \dot{x} \right) G + F \left( \frac{\partial G}{\partial x} \delta x + \frac{\partial G}{\partial \dot{x}} \delta \dot{x} \right)$$ $$= \delta F \cdot G + F \cdot \delta G$$

Advanced: Thm. 3: Multiplying and Dividing Function \(F\) by Another Function \(G\) Does Not Affect the Variation $$\delta F = \delta \left( F \cdot \frac{G}{G} \right) = \delta \left( F \cdot G \cdot G^{-1} \right)$$ $$= \delta F \cdot G \cdot G^{-1} + F \cdot \delta G \cdot G^{-1} + F \cdot G \cdot \delta (G^{-1})$$ $$= \delta F + F \cdot \delta G \cdot G^{-1} + F \cdot G \cdot \left( -\frac{\delta G}{G^2} \right)$$ $$= \delta F$$

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.