Action Principle (Relativistic)

In the relativistic case, to describe a free particle, we use the 4-displacement $$\eta =\eta ^\mu \hat{e} _\mu =(\tau ,\overrightarrow{0} )_{porper}=(t,\overrightarrow{\eta})$$ to describe the trajectory of the particle, where \(\tau\) is the particle's proper time. Here, \(\eta ^\mu\) is used to distinguish the trajectory from spacetime (to accommodate subsequent discussions on Noether's theorem, it is necessary to rigorously distinguish between the trajectory and spacetime; the trajectory is a physical quantity, while spacetime is a coordinate system, which are different concepts). To describe the particle's velocity, we use the 4-Velocity \(U=U^\mu \hat{e} _\mu =(\gamma c,\gamma \overrightarrow{v} )={d\eta ^\mu \over d\tau} \hat{e} _\mu\), where \(\tau\) is the particle's proper time. Furthermore, \(U^\mu =U^\mu (x^\nu )\), meaning that the velocity \(U^\mu\) changes with different coordinates \(x^\nu\) in spacetime. The idea here is that a free particle moves from point a to point b in spacetime, and we calculate the extremum of the Action \(S_P\) for different paths \(\eta ^\mu\) by varying \(x^\mu\): 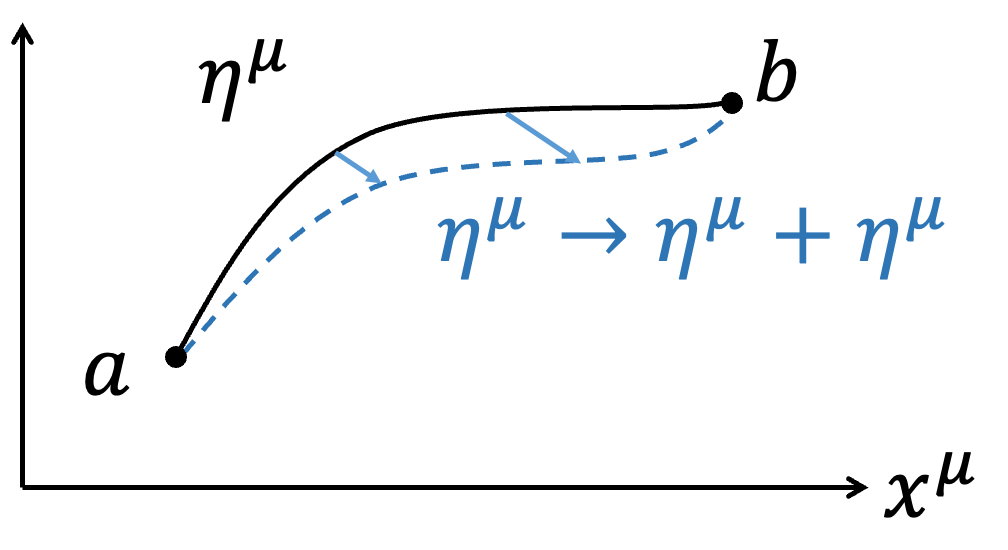$$\eta ^\mu \to \eta ^\mu +\delta \eta ^\mu $$ $$\delta \eta ^\mu (a)=\delta \eta ^\mu (b)=0$$ The Action \(S_P\) for a free particle is: $$S_P=\int _a^b -mc^2 d\tau $$ After variation: $$\delta S_P=\delta \int _a^b -mc^2 d\tau =-mc^2 \int _a^b \delta d\tau $$ It may seem that \(d\tau \) is unrelated to the variation \(\eta ^\mu \to \eta ^\mu +\delta \eta ^\mu\), but recall: $$∵c^2 d\tau ^2=d\eta ^\mu d\eta _\mu $$ $$∴cd\tau =\sqrt{d\eta ^\mu d\eta _\mu}$$ Thus: $$\delta S_P=-mc\int _a^b \delta \sqrt{d\eta ^\mu d\eta _\mu}$$ $$=-mc\int _a^b {1\over 2} {\color{red}{\delta d\eta ^\mu \cdot d\eta _\mu +d\eta ^\mu \cdot \delta d\eta _\mu} \over \sqrt{d\eta ^\mu d\eta _\mu}} $$

Advanced: Thm.4: The variation of a scalar is independent of the indices. Recall the metric tensor \(g_{\mu \nu}\): $$g_{\mu \nu} =\hat{e} _\mu \cdot \hat{e} _\nu $$ $$g_{\mu \nu} =g_\nu \mu $$ $$g^{\mu \nu} \equiv (g_{\mu \nu} )^{-1}$$ \(g^{\mu \nu} g_{\nu \omega} = \delta ^\mu _\omega \) (Delta function, do not confuse it with the variation \(\delta\)). The metric tensor \(g_{\mu \nu}\) is an intrinsic property of spacetime (Intrinsic Property) and is independent of \(x^\mu\) (only considering special relativity here; in general relativity, it would be affected). This means that the variation with respect to \(x^\mu\) is independent of the metric \(g_{\mu \nu}\). The metric tensor can be used to raise or lower indices (Index lowering or raising): $$x^\mu =g^{\mu \nu} x_\nu $$ $$x_\mu =g_{\mu \nu} x^\nu $$ Since the variation with respect to \(x^\mu\) is independent of the metric \(g_{\mu \nu}\), we have: $$\delta x^\mu =g^{\mu \nu} \delta x_\nu$$ $$\delta x_\mu =g_{\mu \nu} \delta x^\nu $$ For a scalar, such as \(x^\mu y_\mu \), the variation is: $$\delta (x^\mu y_\mu )=\delta x^\mu \cdot y_\mu +x^\mu \cdot \delta y_\mu $$ $$=g^{\mu \nu} \delta x_\nu \cdot g_{\mu \omega} y^\omega +g^{\mu \nu} x_\nu \cdot g_{\mu \omega} \delta y^\omega $$ $$=g^{\mu \nu} g_{\mu \omega} (\delta x_\nu \cdot y^\omega +x_\nu \cdot \delta y^\omega )=g^{\color{red}{\nu \mu}} g_{\mu \omega} \delta (x_\nu y^\omega )$$ $$= \delta ^\nu _\omega \delta (x_\nu y^\omega )=\delta (x_\omega y^\omega )=\delta (x_\mu y^\mu )$$ Similarly: $$x^\mu \delta y_\mu =x_\mu \delta y^\mu $$ Therefore: $$\color{red}{\delta dx^\mu \cdot dx_\mu +dx^\mu \cdot \delta dx_\mu} $$ $$=\delta dx^\mu \cdot dx_\mu +dx_\mu \cdot \delta dx^\mu $$ $$=2\delta dx^\mu \cdot dx_\mu $$

$$\delta S_P=-mc\int _a^b {1\over 2} {2\delta d\eta ^\mu\cdot d\eta _\mu \over \sqrt{d\eta ^\mu d\eta _\mu}} $$ $$= -mc\int _a^b {\delta d\eta ^\mu \cdot d\eta _\mu \over cd\tau}$$ $$ =-m\int _a^b \delta d\eta ^\mu \cdot U_\mu $$ Using the method of Thm.1, we exchange \(\delta dx^\mu \) with \(d\delta x^\mu\), and perform integration by parts: $$\delta S_P=-m\int _a^b U_\mu d\delta \eta ^\mu $$ $$=\color{red}{ -\left[ U_\mu \delta \eta ^\mu \right]\Big| _a^b}+m\int _a^b dU_\mu \delta \eta ^\mu$$ The boundary term is zero because the boundary variation \(\delta \eta ^\mu (a)=\delta \eta ^\mu (b)=0\). The latter term can be multiplied and divided by \(d\tau\) without affecting the variation, according to Thm.3: $$\delta S_P=m\int _a^b dU_\mu \delta \eta ^\mu $$ $$ =\int _a^b {m (dU_\mu )\over d\tau} \delta \eta ^\mu d\tau $$ So, for a free particle, \(\delta S_P=0\) leads to: \(m {dU_\mu \over d\tau} =0\) Considering \(\mu =1\sim 3\): $$m {d\overrightarrow{v}\over d\tau} =0$$ A free particle has no acceleration and maintains uniform motion.

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.