Action Principle (Relativistic)

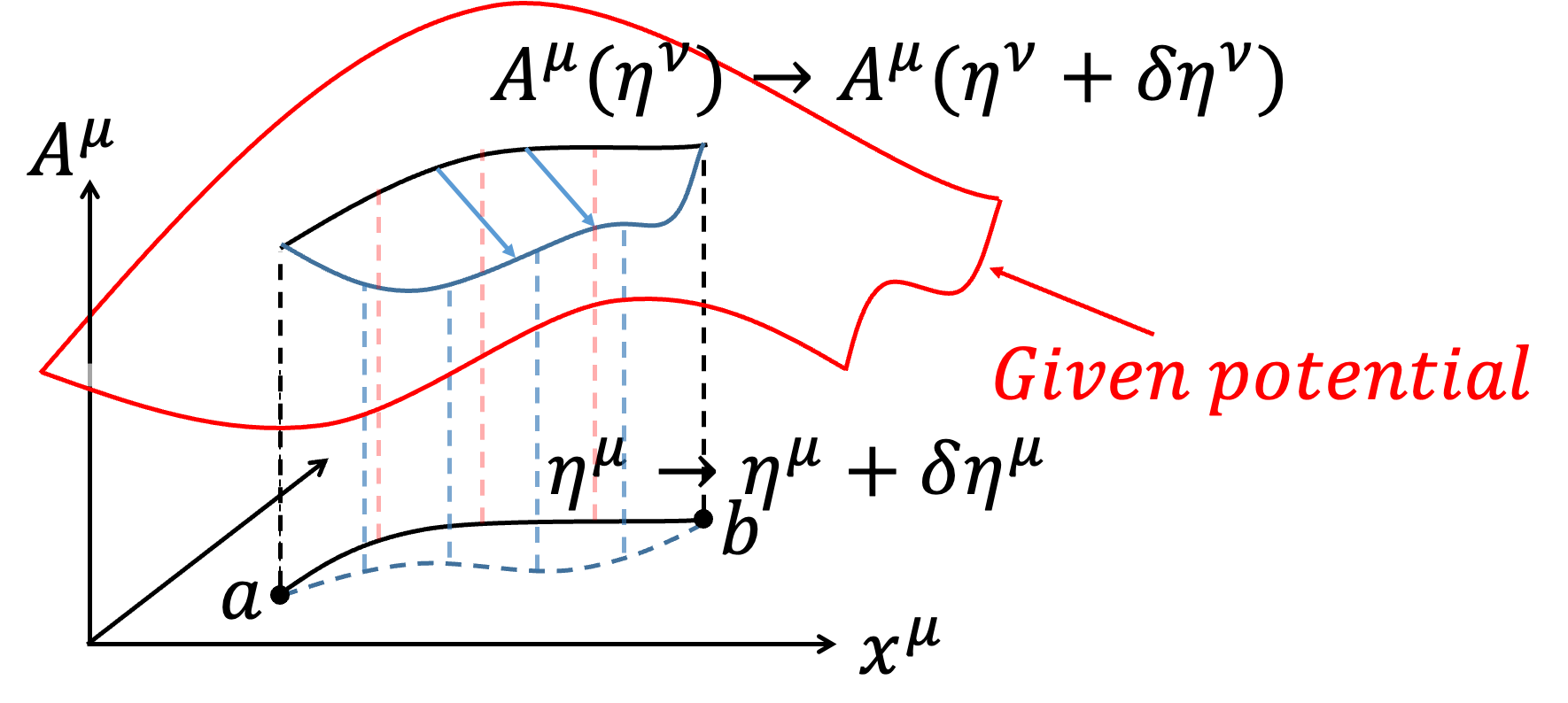
In this section, we aim to explore how a charged particle moves under a given EM Field (note that "given EM Field" means we do not vary the EM Field itself). In relativistic electrodynamics, we write the 4-Potential as \(A = A^\mu \hat{e} _\mu =\left(\phi,\overrightarrow{A}\right)\), using Gaussian units here. The Action \(S_{PF}\) for the interaction of the charged particle is written as: $$S_{PF}=\int _a^b -{e \over c} A_\mu d\eta ^\mu $$ The complete description of the motion of the charged particle is given by: $$S=S_P+S_{PF}=\int _a^b -mc^2 d\tau +\int _a^b -{e\over c} A_\mu d\eta ^\mu $$ Here, we consider varying the path \(\eta ^\mu\) of the charged particle in spacetime: $$\eta ^\mu \to \eta ^\mu +\delta \eta ^\mu $$ Although we do not vary the EM Field \(A^\mu\), the potential experienced by the particle depends on the path taken. Hence, the Action for different paths will involve different values of \(A^\mu\) (meaning the change in \(A^\mu\) comes from the different paths \(\eta ^\mu\) rather than from varying \(A^\mu\)): $$A^\mu (\eta ^\mu )\to A^\mu (\eta ^\mu +\delta \eta ^\mu )=A^\mu (\eta ^\mu )+\delta A^\mu $$

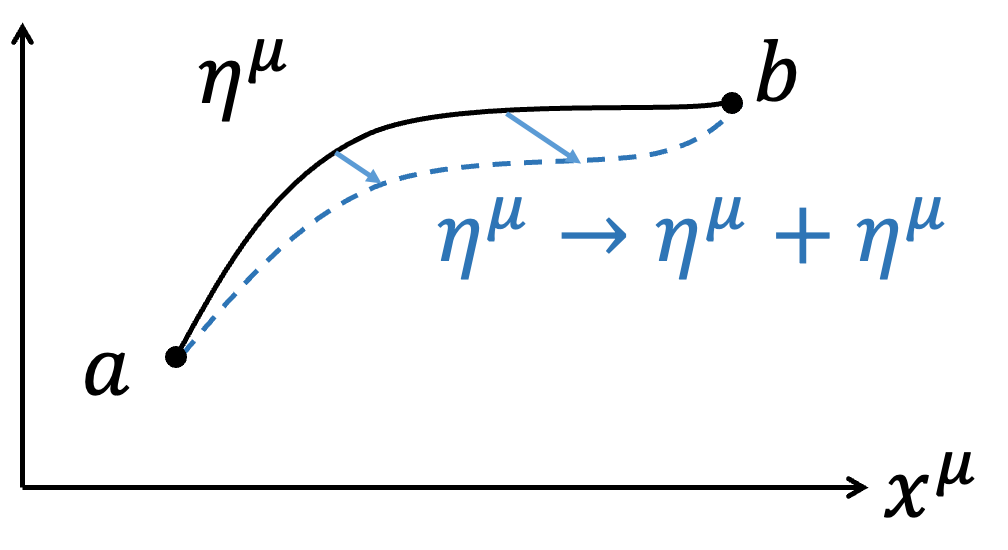We calculate how \(\delta S_{PF}\) varies: $$\delta S_{PF}=\delta \int _a^b -{e\over c} A_\mu d\eta ^\mu $$ $$ =-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu -{e\over c} \int _a^b A_\mu \cdot \delta d\eta ^\mu $$ Using the method of Thm.1, we exchange \(\delta d\eta ^\mu \) with \(d\delta \eta ^\mu\): $$\delta d\eta ^\mu =d\delta \eta ^\mu $$ and perform integration by parts, where the boundary term vanishes: $$\delta S_{PF}=-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu -{e\over c} \int _a^b A_\mu \cdot d\delta \eta ^\mu $$ $$ =-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu \color{red}{ -\left[{e\over c} A_\mu \cdot \delta \eta ^\mu \right] \Big|_a^b}+{e\over c} \int _a^b dA _\mu \cdot \delta \eta ^\mu $$ Using Thm.3, multiplying and dividing by \(d\tau \) does not affect the variation: $$\delta S_{PF}=-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu +{e\over c} \int _a^b dA _\mu \cdot \delta \eta ^\mu $$ $$ =-{e\over c} \int _a^b \delta A_\mu \cdot {d\eta ^\mu \over \color{red}{d\tau}} \color{red}{d\tau} +{e\over c} \int _a^b {dA _\mu \over \color{red}{d\tau}} \color{red}{d\tau} \cdot \delta \eta ^\mu $$ Since: $$\delta A_\mu ={\partial A_\mu \over \partial x ^\nu } \delta \eta ^\nu $$ and $${dA_\mu \over d\tau} ={\partial A_\mu \over \partial x^\nu } {d\eta ^\nu \over d\tau} ={\partial A_\mu \over \partial x^\nu } U^\nu $$ Substituting these, we get: $$\delta S_{PF}=-{e\over c} \int _a^b {\partial A_\mu \over\partial x^\nu } \delta \eta ^\nu \cdot u^\mu d\tau +{e\over c} \int _a^b {\partial A_\mu \over \partial x^\nu } U^\nu d\tau \cdot \delta \eta ^\mu$$ $$=-{e\over c} \int _a^b (\partial _\nu A_\mu ) u^\mu \delta \eta ^\nu d\tau +{e\over c} \int _a^b \left(\partial _\nu A_\mu \right) U^\nu \delta \eta ^\mu d\tau $$ We want to factor out the variation \(\delta \eta ^\nu \) and \(\delta \eta ^\mu\) together, but the indices do not match. However, since each term's indices \(\mu\) and \(\nu\) are dummy indices, we can interchange them \(\mu \leftrightarrow \nu\). By swapping \(\mu\) and \(\nu\) in the first term, we can combine the terms: $$\delta S_{PF}=-{e\over c} \int _a^b \left( \partial _{\color{red}{\mu}} A_{\color{red}{\nu}} \right) U^{\color{red}{\nu}} \delta \eta ^{\color{red}{\mu}} d\tau +{e\over c} \int _a^b (\partial _\nu A_\mu ) U^\nu \delta \eta ^\mu d\tau $$ $$=-{e\over c} \int _a^b (\partial _\mu A_\nu -\partial _\nu A_\mu ) U^\nu \delta \eta ^\mu d\tau $$ Considering the full motion of the charged particle in the EM Field: $$\delta S=\delta S_P+\delta S_{PF}=0$$ Thus: $$\delta S_P+\delta S_{PF}=\int _a^b m {dU_\mu \over d\tau} \delta \eta ^\mu d\tau -{e\over c} \int _a^b \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu \delta \eta ^\mu d\tau $$ $$=\int _a^b \left[m {dU_\mu \over d\tau} -{e\over c} \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu \right] \delta \eta ^\mu d\tau =0$$ We obtain: $$m {dU_\mu \over d\tau} -{e\over c} \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu =0$$ $$m {dU_\mu \over d\tau} ={e\over c} \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu \equiv {e\over c} F_{\mu \nu} U^\nu $$ We define the electromagnetic tensor: $$F_{\mu \nu} =\partial _\mu A_\nu -\partial _\nu A_\mu $$ The relationship between the electric field \(\overrightarrow{E}\), the magnetic field \(\overrightarrow{B}\), and the potentials \(\phi\), \(\overrightarrow{A}\) (in Gaussian units): $$ \overrightarrow{E}=-\nabla \phi-{1\over c} {\partial \overrightarrow{A}\over \partial t}$$ $$\overrightarrow{B}=\nabla \times \overrightarrow{A} $$ Where: $$A_\nu \to \left(\phi,-A_x,-A_y,-A_z \right)$$ $$\partial _\mu \to \left({\partial \over \partial x^0},{\partial \over \partial x^1 },{\partial \over \partial x^2},{\partial \over \partial x^3 }\right)=\left({\partial \over \partial ct},{\partial \over \partial x },{\partial \over \partial y},{\partial \over \partial z }\right)$$ We can calculate: $$F_{\mu \nu} =\partial _\mu A_\nu -\partial _\nu A_\mu =\left(\begin{matrix}0 & E_x & E_y & E_z\\ -E_x & 0 & -B_z & B_y \\ -E_y & B_z & 0 & -B_x \\ -E_z & -B_y & B_x & 0 \end{matrix}\right)$$ $$F^{\mu \nu} =\partial ^\mu A^\nu -\partial ^\nu A^\mu =\left(\begin{matrix}0 & -E_x & -E_y & -E_z\\ E_x & 0 & -B_z & B_y \\ E_y & B_z & 0 & -B_x \\ E_z & -B_y & B_x & 0 \end{matrix}\right)$$

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.