Action Principle (Relativistic)

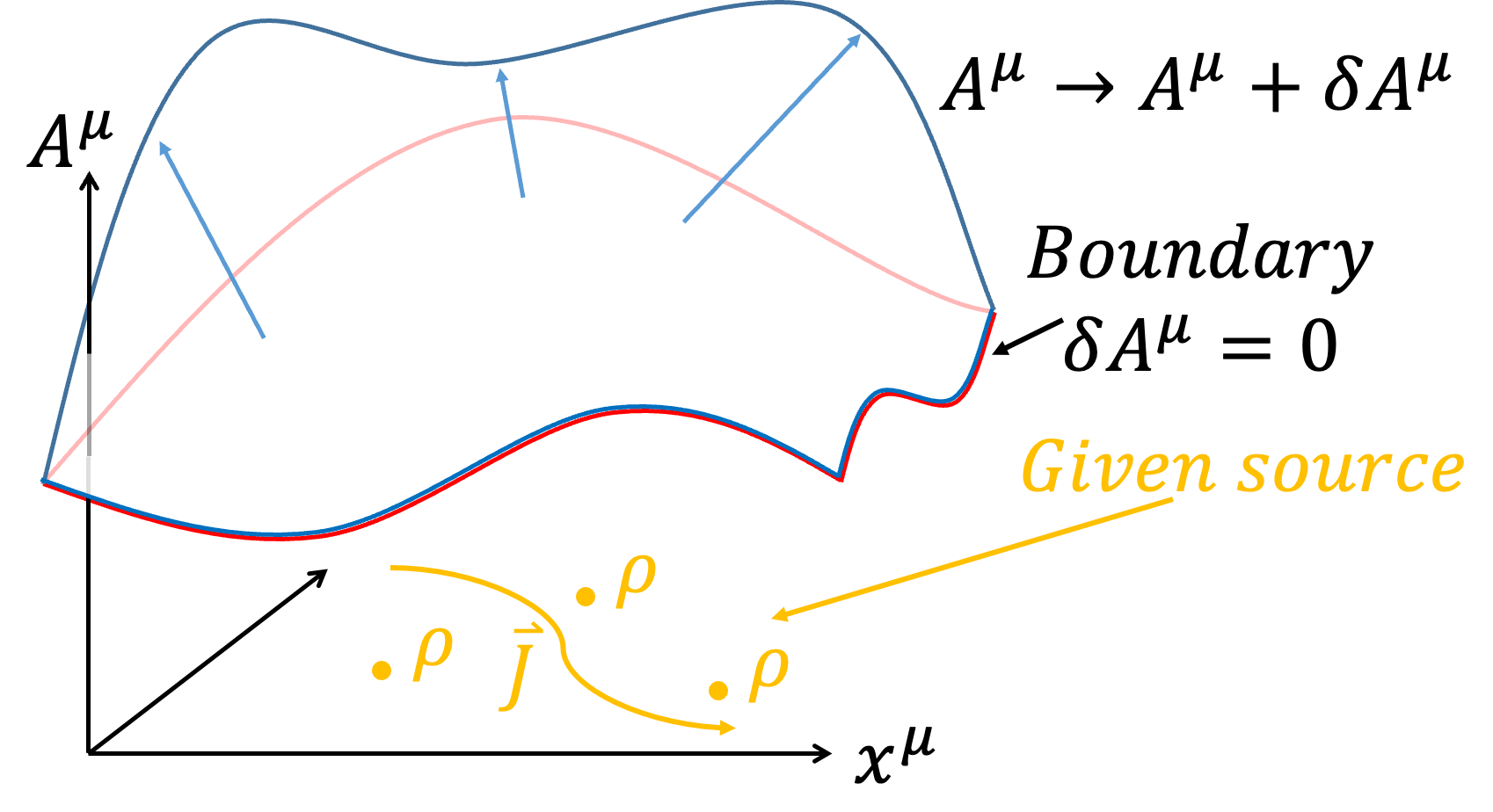
In this section, we discuss the distribution of the EM Field given a source (meaning we do not vary the distribution \(\eta^\mu\) of the source). The relevant action is: $$S_{PF}+S_F=\int -\rho_m c-{1\over c^2} A_\mu J^\mu d^4 x +\int -{1 \over 16\pi c} F_{\mu \nu} F^{\mu \nu} d^4 x$$ To understand the distribution of the EM Field, we vary \(A^\mu\): $$A^\mu \to A^\mu +\delta A^\mu $$ We observe whether \(J^\mu\), \(d^4 x\), or \(F^{\mu \nu}\) are affected:

$$J^\mu =\rho_e {dx^\mu \over d\tau} =J^\mu (x^\nu )$$ $$d^4 x=d^4 x(x^\nu )$$ $$F^{\mu \nu} =\partial ^\mu A^\nu -\partial ^\nu A^\mu =F^{\mu \nu} \left(A^\omega \right)$$ Only the electromagnetic tensor \(F^{\mu \nu}\) is affected by the variation \(A^\mu \to A^\mu +\delta A^\mu\): $$F^{\mu \nu} \left(A^\omega \right)\to F^{\mu \nu} (A^\omega +\delta A^\omega )=F^{\mu \nu} \left(A^\omega \right)+\delta F^{\mu \nu} $$ Thus, the variation of \(S_{PF}\) is straightforward: $$\delta S_{PF}=\delta \int -{1 \over c^2} A_\mu J^\mu d^4 x$$ $$ =-{1 \over c^2} \int \delta A_\mu \cdot J^\mu d^4 x $$ The variation of \(S_F\) is more complex: $$S_F=-{1 \over 16 \pi c} \int F_{\mu \nu} F^{\mu \nu} d^4 x$$ $$\delta S_F=-{1 \over 16 \pi c} \delta \int F_{\mu \nu} F^{\mu \nu} d^4 x =-{1 \over 16 \pi c} \int \delta F_{\mu \nu} \cdot F^{\mu \nu} +F_{\mu \nu} \cdot \delta F ^{\mu \nu} d^4 x $$ Using Thm.4 (variation of scalars is independent of upper and lower indices): $$\delta F_{\mu \nu} \cdot F^{\mu \nu} =F_{\mu \nu} \cdot \delta F ^{\mu \nu}$$ Hence, there is a factor of two: $$\delta S_F=-{1 \over 16 \pi c} \int 2\delta F_{\mu \nu} \cdot F^{\mu \nu} d^4 x =-{1 \over 8 \pi c} \int \delta F_{\mu \nu} \cdot F^{\mu \nu} d^4 x $$ Substitute: $$\delta S_F=-{1 \over 8 \pi c} \int \delta (\partial _\mu A_\nu -\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ $$=-{1 \over 8 \pi c} \int \delta (\partial _\mu A_\nu )\cdot F^{\mu \nu} d^4 x +{1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ Since \(\mu\) and \(\nu\) are dummy indices, we can swap \(\mu \leftrightarrow \nu\) in the first term: $$\delta S_F=-{1 \over 8 \pi c} \int \delta (\partial _{\color{red}{\nu}} A_{\color{red}{\mu}} )\cdot F^{\color{red}{\nu \mu}} d^4 x +{1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ $$={1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot (-F^\nu \mu +F^{\mu \nu} ) d^4 x $$ Recall the electromagnetic tensor: $$F^{\mu \nu} =\partial ^\mu A^\nu -\partial ^\nu A^\mu =\left(\begin{matrix}0 & -E_x & -E_y & -E_z\\ E_x & 0 & -B_z & B_y \\ E_y & B_z & 0 & -B_x \\ E_z & -B_y & B_x & 0 \end{matrix}\right)$$ Since \(F^{\mu \nu}\) is an antisymmetric tensor, \(F^\nu \mu =-F^{\mu \nu} \). Substituting: $$\delta S_F={1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot (F^{\color{red}{\mu \nu}} +F^{\mu \nu} ) d^4 x ={1 \over 4 \pi c} \int \delta (\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ Using Thm.1, we can exchange \(\delta\) and \(\partial _\nu\): $$\delta (\partial _\nu A_\mu )=\partial _\nu (\delta A_\mu )$$ $$\delta S_F={1 \over 4 \pi c} \int \partial _\nu (\delta A_\mu )\cdot F^{\mu \nu} d^4 x $$ Using the chain rule: $$\partial _\nu (\delta A_\mu )\cdot F^{\mu \nu} =\partial _\nu (\delta A_\mu \cdot F^{\mu \nu} )-\delta A_\mu \cdot \partial _\nu (F^{\mu \nu} )$$ Splitting the integral into two parts: $$\delta S_F={1 \over 4 \pi c} \int \partial _\nu (\delta A_\mu \cdot F^{\mu \nu} ) d^4 x -{1 \over 4 \pi c} \int \delta A_\mu \cdot \partial _\nu (F^{\mu \nu} ) d^4 x $$

Recall the Divergence Theorem: $$\int \nabla \cdot \overrightarrow{F}dV =∮ \overrightarrow{F}\cdot d\overrightarrow{S} $$ A volume integral can be rewritten as a surface integral. Written in terms of the Levi-Civita symbol: $$\int \partial _\nu F^\nu dV =∮ F^\nu dS_\nu $$

Thus, using the Divergence Theorem, the first term vanishes since the variation \(\delta A_\mu\) on the boundary is zero: $${1 \over 4 \pi c} \int \partial _\nu (\delta A_\mu \cdot F^{\mu \nu} ) d^4 x ={1 \over 4 \pi c} ∮ \delta A_\mu \cdot F^{\mu \nu} dS_\nu =0$$ Therefore: $$\delta S_F=-{1 \over 4 \pi c} \int \partial _\nu (F^{\mu \nu} )\cdot \delta A_\mu d^4 x $$ Combining \(\delta S_{PF} + \delta S_F\): $$\delta S_{PF}+\delta S_F=-{1 \over c^2} \int J^\mu \cdot \delta A_\mu d^4 x -{1 \over 4 \pi c} \int \partial _\nu (F^{\mu \nu} )\cdot \delta A_\mu d^4 x$$ $$=\int \left[-{1 \over c^2} J^\mu -{1 \over 4 \pi c} \partial _\nu F^{\mu \nu} \right]\delta A_\mu d^4 x =0$$ Thus, we obtain: $$-{1 \over c^2} J^\mu -{1 \over 4 \pi c} \partial _\nu F^{\mu \nu} =0$$ $$\partial _\nu F^{\mu \nu} =-{4\pi \over c} J^\mu $$

Recall Maxwell's equations in Gaussian units: $$ \nabla \cdot \overrightarrow{E}=4\pi \rho_e$$ $$ \nabla \cdot \overrightarrow{B}=0$$ $$ \nabla ×\overrightarrow{E}=-{1 \over c} {\partial \overrightarrow{B} \over \partial t}$$ $$ \nabla ×\overrightarrow{B}={4\pi \over c} \overrightarrow{J}+{1 \over c} {\partial \overrightarrow{E} \over \partial t }$$

$$\partial _\nu F^{\mu \nu} =-{4\pi \over c} J^\mu \to \left( \begin{matrix} \nabla \cdot \overrightarrow{E}=4\pi \rho_e \\ \nabla ×\overrightarrow{B}={4\pi \over c} \overrightarrow{J}+{1 \over c} {\partial \overrightarrow{E}\over \partial t} \end{matrix}\right)$$

$$F_{\mu \nu} =\partial _\mu A_\nu -\partial _\nu A_\mu $$ The electromagnetic tensor has a special identity (Bianchi identity): $$\partial _\omega F_{\mu \nu} +\partial _\mu F_{\nu \omega} +\partial _\nu F_{\omega \mu} =\partial _{[\omega} F_{\mu \nu ]} =0$$ Expanding: $$\partial _\omega (\partial _\mu A_\nu -\partial _\nu A_\mu )+\partial _\mu (\partial _\nu A_\omega -\partial _\omega A_\nu )+\partial _\nu (\partial _\omega A_\mu -\partial _\mu A_\omega )=0$$ $$\partial _\omega \partial _\mu A_\nu -\partial _\omega \partial _\nu A_\mu +\partial _\mu \partial _\nu A_\omega -\partial _\mu \partial _\omega A_\nu +\partial _\nu \partial _\omega A_\mu -\partial _\nu \partial _\mu A_\omega =0$$ This relation yields:

$$ \partial _\omega F_{\mu \nu} +\partial _\mu F_{\nu \omega} +\partial _\nu F_{\omega \mu} =0 \to \left( \begin{matrix} \nabla \cdot \overrightarrow{B}=0 \\ \nabla ×\overrightarrow{E}=-{1 \over c} {\partial \overrightarrow{B} \over \partial t} \end{matrix}\right)$$

Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.