Continuous Fields and the Wave Equation
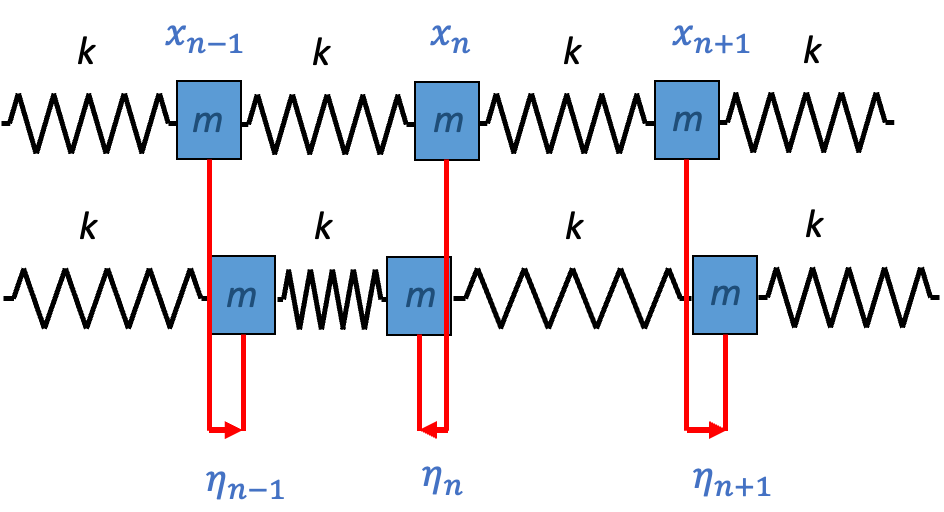
Transitioning from a single particle to a continuous field, physicists describe a continuous field by linking an infinite number of harmonic oscillators. For an infinite number of harmonic oscillators, we can write the Lagrangian:
$$\mathcal{L}=∑_n^\infty {1 \over 2} m\eta ̇_n-{1 \over 2} k(\eta _n-\eta _(n-1) )^2 $$
Where \(\eta_n\) is the amplitude at position \(n\), and \(\eta ̇_n\) is the velocity of oscillation at position \(n\).

In the continuous field, the Lagrangian is:
$$\mathcal{L}=\int {1 \over 2} \rho\left({\partial \eta \over\partial t}\right)^2-{1 \over 2} Y\left({\partial \eta \over\partial x}\right)^2 dx $$
Where \(\rho\) is the mass density, and \(Y\) is the Young's modulus.

In three dimensions, the Lagrangian is:
$$\mathcal{L}=\int {1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2 dV$$
It is evident that the Lagrangian density \(\mathcal{L}={1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2\). Similarly, we can use the variational principle to obtain the equation of motion for the continuous field. The action is:
$$S=\int Ld^4 x =\int {1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2 d^4 x $$
Varying the field amplitude \(\eta (x^\mu )\to \eta (x^\mu )+\delta \eta (x^\mu )\), the action should be an extremum:
$$\delta S=\delta \int {1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2 d^4 x $$
$$=\int \rho\partial _t \eta *\delta (\partial _t \eta )-Y \nabla \eta *\delta ( \nabla \eta ) d^4 x $$
Exchanging the variation and differentiation:
$$=\int \rho\partial _t \eta \partial _t (\delta \eta )-Y \nabla \eta \nabla (\delta \eta ) d^4 x $$
$$=\int \rho\partial _t \eta \partial _t (\delta \eta ) d^4 x -\int Y \nabla \eta \nabla (\delta \eta ) d^4 x $$
$$=\int \partial _t (\rho\partial _t \eta \delta \eta ) d^4 x -\int \partial _t (\rho\partial _t \eta )*\delta \eta d^4 x -\int \nabla (Y \nabla \eta \delta \eta ) d^4 x +\int \nabla (Y\eta )*\delta \eta d^4 x $$
$$=\left[-\int \partial _t (\rho\partial _t \eta )*\delta \eta d^4 x +\int \nabla (Y\eta )*\delta \eta d^4 x \right]+\left[\int \partial _t (\rho\partial _t \eta \delta \eta ) d^4 x -\int \nabla (Y \nabla \eta \delta \eta ) d^4 x \right]$$
The boundary terms, using integration by parts, give:
$$=-\int \left[\rho\partial _t^2 \eta -Y \nabla ^2 \eta \right]*\delta \eta d^4 x +\left[\int \rho\partial _t \eta \delta \eta d^3 x \Big|_{t_1}^{t_2}- \int Y \nabla \eta \delta \eta d^3 x \Big|_{\partial x,\partial y,\partial z} \right]$$
$$=-\int [\rho\partial _t^2 \eta -Y \nabla ^2 \eta ]*\delta \eta d^4 x +0$$
Since \(\delta \eta\) is arbitrary, we obtain:
$$\rho\partial _t^2 \eta -Y \nabla ^2 \eta =0$$
$$ \nabla ^2 \eta ={\rho \over Y} \partial _t^2 \eta $$
Setting \(v=\sqrt{{Y\over \rho}}\):
$$\nabla ^2 \eta ={1\over v^2} \partial _t^2 \eta $$
This is the wave equation.
Originally written in Chinese by the author, these articles are translated into English to invite cross-language resonance.
 Peir-Ru Wang
Peir-Ru Wang