最小作用量原理（古典）

前一部分介紹了簡單的變分法概念，但是需要引入任意的函數\(\eta (t)\)，手法上稍嫌煩瑣，不利於後續操作。第二部分以相同的概念，採用比較抽象的想法但相同的數學手法，演示一次變分法的操作。有點像將變分的操作類同於微分操作。

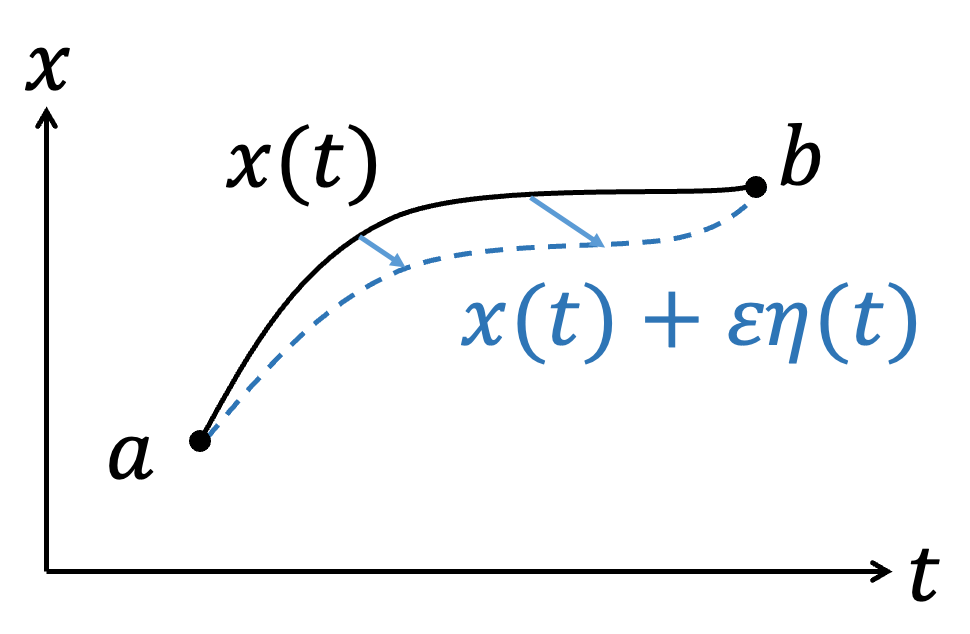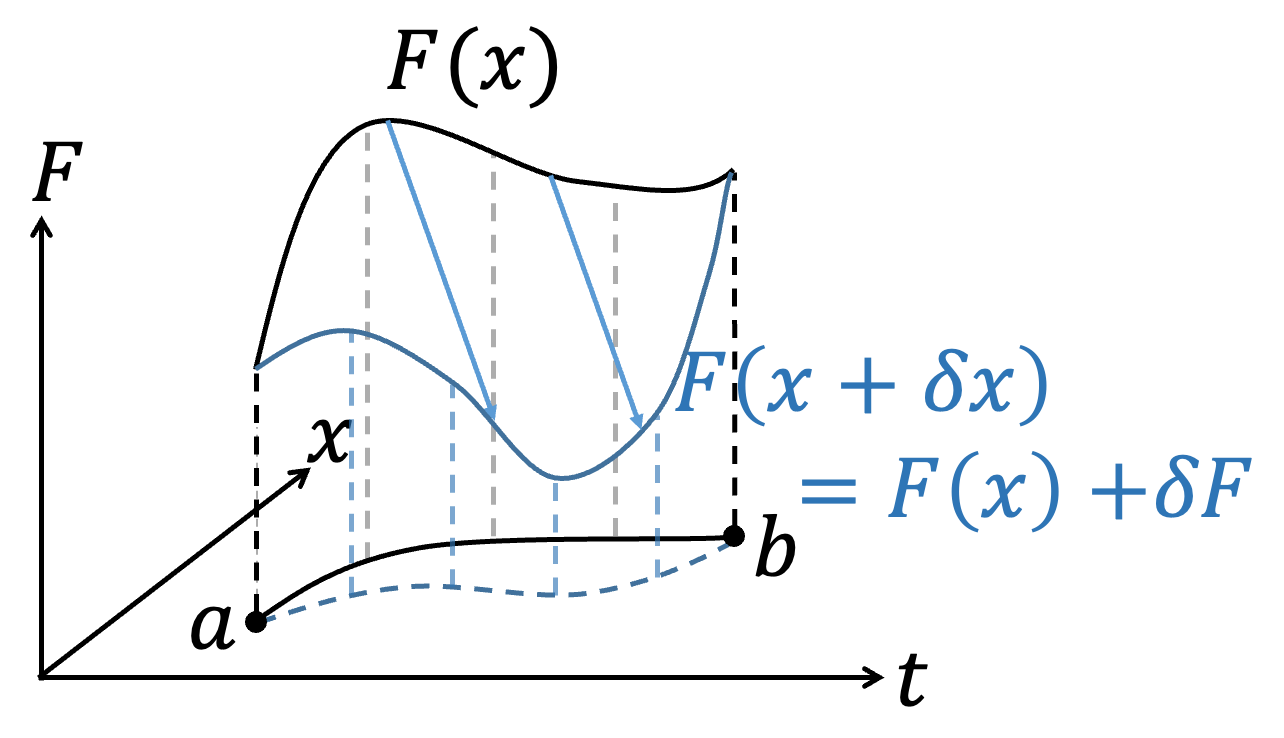針對同一種泛函（Functional）的積分問題 $$S[F(x,\dot{x},t)]=\int_a^b F(x,\dot{x},t)dt $$ 當我們針對\(x\)做變分， $$x→x+\delta x$$ 變分\(\delta x\)滿足 $$\delta x(a)=\delta x(b)=0$$ \(x\)的變分會導致\(\dot{x}\)、\(F\)發生變化 $$ \dot{x} (x) \to \dot{x} (x+\delta x) =\dot{x}(x)+\delta \dot{x}$$ $$F(x,\dot{x},t)→F(x+\delta x,\dot{x}(x)+\delta \dot{x},t)=F(x,\dot{x},t)+\delta F $$ 我們要\(\delta S=0\) $$\delta S=\delta \int _a^b Fdt=\int _a^b \delta Fdt=0$$ 概念上很好理解的是，\(\delta F\)的變化和\(\delta x\)、\(\delta \dot{x}\)有關，所以將\(\delta F\)展開 $$\delta S=\int _a^b \delta Fdt=\int _a^b { \partial F\over\partial x }\delta x+{\partial F\over \partial \dot{x} } \delta \dot{x} dt $$

進階：Thm.1 :微分與變分對調 如果今天微分與變分針對的對象不同，如對\(t\)微分 \(d \over dt\)、對\(x\)變分\(\delta x\)，則 \(d \over dt\)與\(\delta \)可以對調。 $$\delta \dot{f}=\dot{f} (x+\delta x)-\dot{f}(x)$$ $$= {d \over dt} \left(f(x+\delta x)-f(x)\right)= {d \over dt} \delta f$$

將\(\delta \dot{x}\)對調 \({d \over dt} \delta x\)
$$\delta S=\int _a^b {\partial F\over\partial x} \delta xdt+ \int _a^b {\partial F\over \partial \dot{x} } \left( {d \over dt} \delta x\right)dt $$ 同樣的手法對第二項做分部積分 $$\int _a^b {\partial F\over \partial \dot{x} } \left( {d \over dt} \delta x\right)dt = \color{red}{{\partial F\over \partial \dot{x} } \delta x \Big|_a^b}-\int _a^b {d \over dt} {\partial F\over \partial \dot{x} } \delta xdt$$ 注意紅色這一項，因為我們要求變分\(\delta x\)滿足\(\delta x(a)=\delta x(b)=0\)，所以\( \color{red}{{\partial F\over \partial \dot{x} } \delta x\Big|_a^b=0}\) $$\delta S=\int _a^b {\partial F\over\partial x} \delta xdt-\int _a^b \left( {d \over dt} {\partial F\over \partial \dot{x} } \right)\delta xdt $$ $$=\int _a^b \left( {\partial F\over\partial x}- {d \over dt} {\partial F\over \partial \dot{x} } \right)\delta xdt=0$$ \(\delta x \) is arbitrary. $$ {\partial F\over\partial x}- {d \over dt} {\partial F\over \partial \dot{x} } =0$$ Euler-Lagrange equation

進階：Thm.2:變分的Chain rule $$\delta (FG)={\partial (FG)\over\partial x} \delta x+{\partial (FG)\over \partial \dot{x} } \delta \dot{x}$$ $$=\left( {\partial F\over\partial x} G+F {\partial G\over\partial x}\right)\delta x+\left( {\partial F\over \partial \dot{x} } G+F {\partial G\over\partial \dot{x}} \right)\delta \dot{x}$$ $$=\left( {\partial F\over\partial x} \delta x+ {\partial F\over \partial \dot{x} } \delta \dot{x} \right)G+F\left({\partial G\over\partial x} \delta x+{\partial G\over\partial \dot{x}} \delta \dot{x} \right)$$ $$= \delta F\cdot G+F\cdot \delta G$$

進階：Thm.3:針對函數F同乘同除另一函數G，不影響變分 $$\delta F=\delta \left(F\cdot {G\over G}\right)=\delta \left(F\cdot G\cdot G^{-1} \right)$$ $$=\delta F\cdot G\cdot G^{-1}+F\cdot \delta G\cdot G^{-1}+F\cdot G\cdot \delta (G^{-1} )$$ $$=\delta F+F\cdot \delta G\cdot G^{-1}+F\cdot G\cdot \left(-{\delta G\over G^2} \right)$$ $$=\delta F$$