超導臨界耦合常數理論

DOI:10.1038/s41598-023-33809-5

我的博士論文主題為「臨界耦合常數對超導性提升的影響」。論文中清楚闡述了：當耦合強度接近臨界耦合常數時，超導穹頂現象會出現。調控聲子頻率 \(\Omega\)、載子數量 \(Z\)、以及施加壓力 \(P\) 是三種提升超導轉變溫度 \(T_c\) 的關鍵手段。我擴展了 BCS-McMillan 理論，整合這三種因素對超導性的影響，形成統一描述。

超導性的量子哈密頓量

超導性的量子哈密頓量為： $$ \hat{H} \left| \Psi \right> =\left[ \sum\limits_{k\sigma} \xi_k \hat{c}_{k\sigma}^\dagger \hat{c}_{k\sigma} + \frac{1}{N}\sum\limits_{kk^\prime} \frac{g_{eff}}{M\Omega^2} \hat{c}_{k\uparrow}^\dagger \hat{c}_{k\downarrow}^\dagger \hat{c}_{-k^\prime \downarrow} \hat{c}_{k^\prime \uparrow} \right] \left| \Psi \right> $$ 可推導出耦合常數 \(\lambda\) 與 \(T_c\) 的明確表達式為： $$ \lambda = { C \sqrt[3]{Zn_{ion}}\over M\Omega ^2} $$ 和 $$ T_c \sim \Omega\cdot \exp\left(-{1 \over \lambda}\right) = \Omega\cdot \exp\left[-{M\Omega ^2 \over C \sqrt[3]{Zn_{ion}}}\right] $$ 其中 \(C\) 為常數，\(M\) 為離子質量，\(Z\) 為原子價數，\(n_{ion}\) 為離子密度。 當對 \(\Omega\) 求導，有： $$ {dT_c \over d\Omega}\sim {T_c \over \Omega}\cdot \left[1-{2\over \lambda}\right] $$ 當 \(\lambda = 2\) 時導數為零，定義對應於聲子頻率的臨界耦合常數為 \(\lambda_c^\Omega = 2\)。類似地，可以推導出另外兩個臨界耦合常數： \(\lambda_c^Z= {5 \over 3}\)，與 \(\lambda_c^P={4 \over 3}\)。

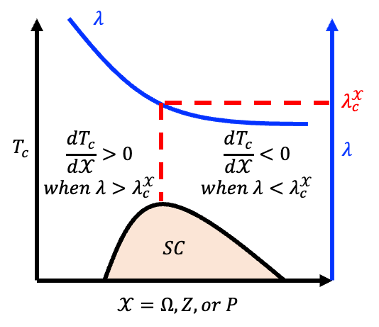
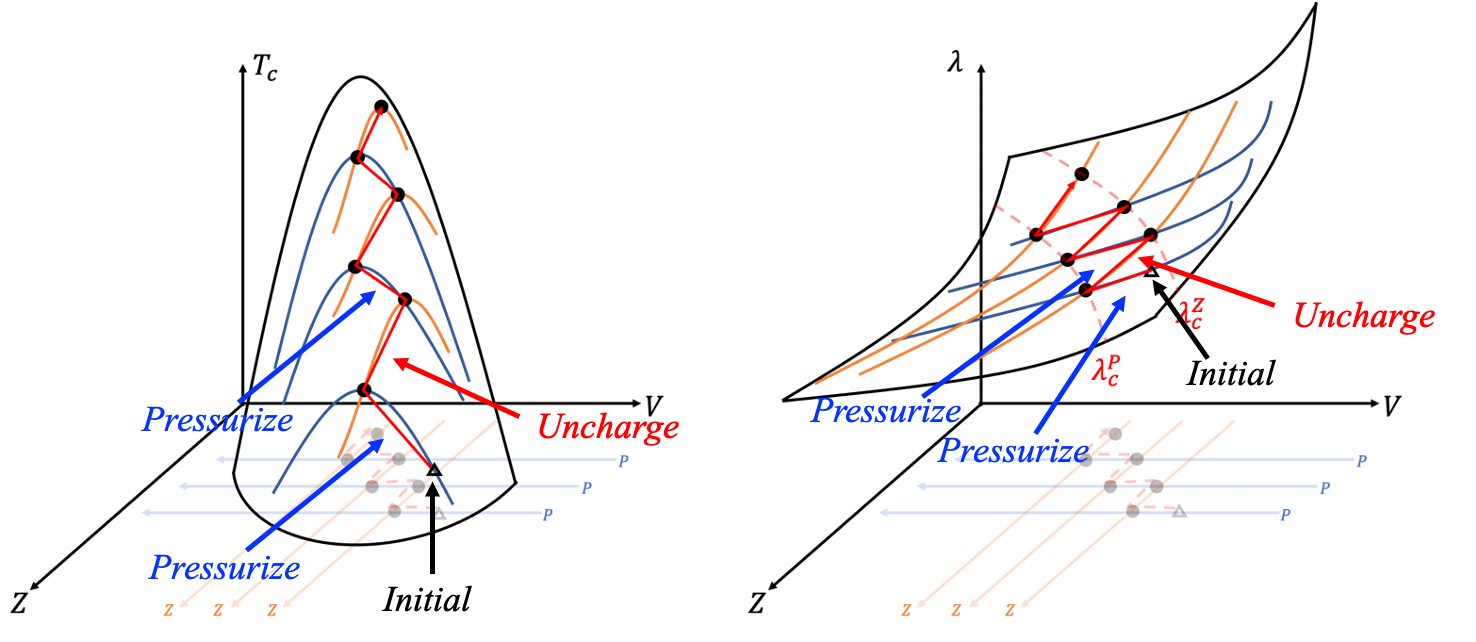
這些臨界耦合常數與實驗結果一致，並可將超導性依據耦合強度分為三類： 弱耦合（\(\lambda_c < \lambda_c^P\)），中等耦合（\(\lambda_c^P < \lambda_c^\Omega\)），與強耦合（\(\lambda_c > \lambda_c^\Omega\)）。 每一區段有對應的不同提升策略，特別的是弱耦合與強耦合區域的提升策略恰好相反， 但最終都會導引超導性進入中等耦合區，並在該區域進一步提升 \(T_c\)。 具體而言，假設耦合常數 \(\lambda\) 位於區間 \(\lambda_c^P<\lambda<\lambda_c^Z\)。此時可透過下列三步驟達成「鋸齒式提升」：
1. 先調整 \(Z\)，使 \(\lambda = \lambda_c^Z\)，稱為 \(\lambda_1\)。
2. 接著增加壓力 \(P\)，會導致 \(\lambda\) 下降，當 \(\lambda = \lambda_c^P\) 時，\(T_c\) 再次被最大化，稱為 \(\lambda_2\)。
3. 這時可以再減少 \(Z\)，提升 \(\lambda\)，當 \(\lambda = \lambda_c^Z\) 時又達到新一波的最大值，稱為 \(\lambda_3\)。 重複第2與第3步驟，即可像「鋸齒式爬山」般逐步提升 \(T_c\)。

根據上述理論，我聚焦於化學設計，包括高頻聲子、複數載子、與小晶格常數。我以 \(Bi_2Sr_2Ca_2Cu_3O_x\) 和 \(YBa_2Cu_3O_x\) 為基礎，合成了一系列高熵氧化物 (HEO) 超導材料，並使用 ZEISS Gemini SEM 與 Bruker D2 PHASER XRD 進行微結構分析。