Charge Particle與EM Field作用下的變分與運動方程
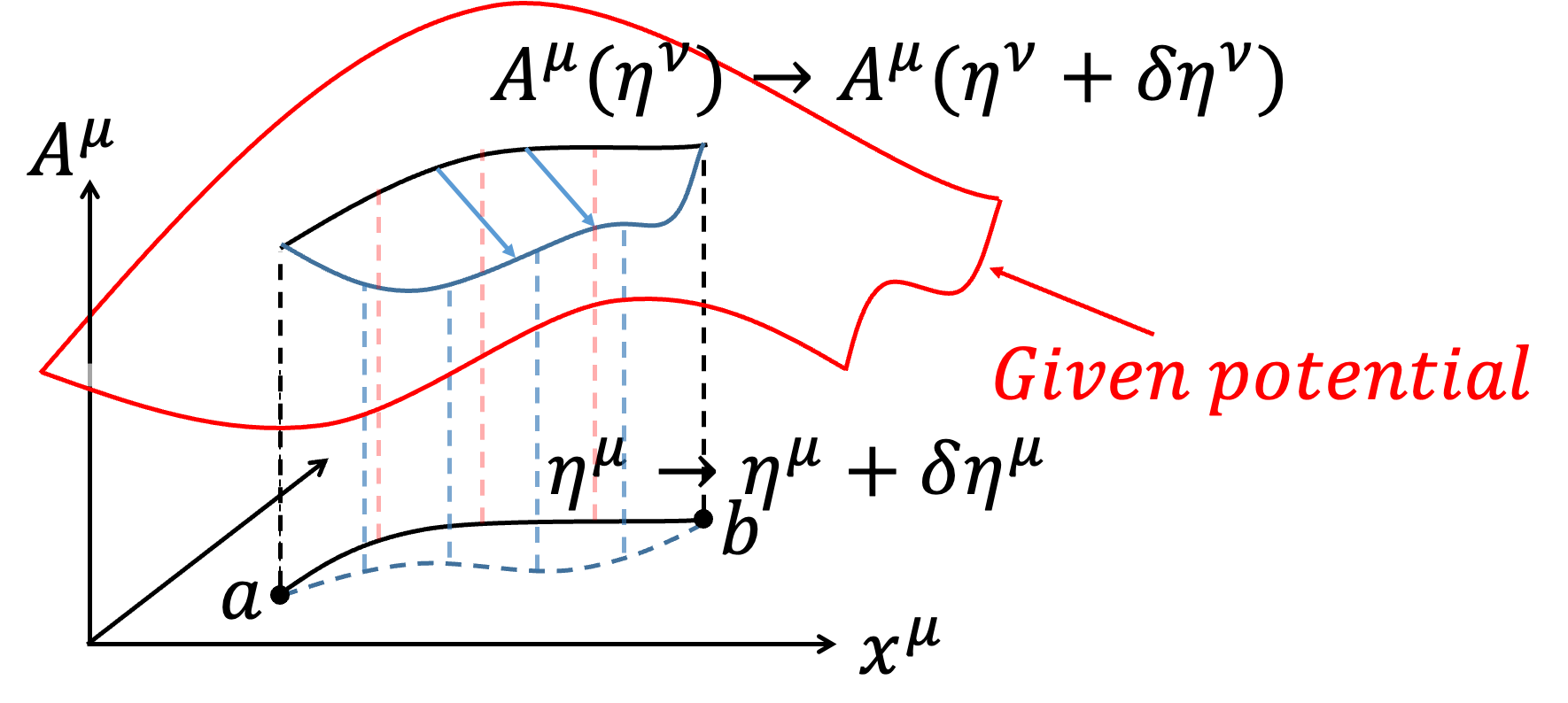
在這一部分中,我們想探討一個Charge Particle在給定的EM Field下如何運動?(注意喔,給定的EM Field表示我們不對EM Field作變分)。相對論性電磁學下我們會寫下4-Potential \(A= A^\mu \hat{e} _\mu =\left(\phi,\overrightarrow{A}\right)\),在這邊採用高斯制(Gaussian unit),而Charge Particle交互作用的Action \(S_{PF}\)會寫成 $$S_{PF}=\int _a^b -{e \over c} A_\mu d\eta ^\mu $$ 完整的描述Charge Particle運動即為 $$S=S_P+S_{PF}=\int _a^b -mc^2 d\tau +\int _a^b -{e\over c} A_\mu d\eta ^\mu $$ 在這邊,我們考慮Charge Particle在時空中的路徑作\(\eta ^\mu\) 變分 $$\eta ^\mu \to \eta ^\mu +\delta \eta ^\mu $$ 雖然我們沒有對EM Field \(A^\mu\) 作變分,但是走不同路徑感受到的位能是不一樣的,所以Action走不同的路徑會有不同的\(A^\mu \)(意思是\(A^\mu \) 的變化來自於路徑 \(\eta ^\mu\) 不同,而不是對\(A^\mu\) 作變分) $$A^\mu (\eta ^\mu )\to A^\mu (\eta ^\mu +\delta \eta ^\mu )=A^\mu (\eta ^\mu )+\delta A^\mu $$
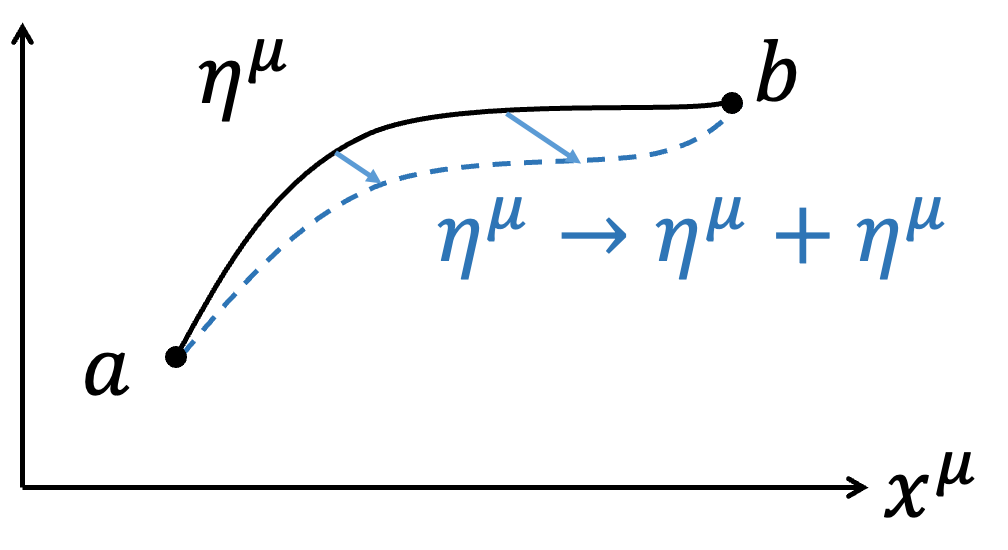 |
 |
我們計算\(\delta S_{PF}\)如何變分:
$$\delta S_{PF}=\delta \int _a^b -{e\over c} A_\mu d\eta ^\mu $$
$$ =-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu -{e\over c} \int _a^b A_\mu \cdot \delta d\eta ^\mu $$
利用Thm.1的方法,我們將\(\delta d\eta ^\mu \)對調\(d\delta \eta ^\mu \)
$$\delta d\eta ^\mu =d\delta \eta ^\mu $$
並作分部積分,邊界項會消失
$$\delta S_{PF}=-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu -{e\over c} \int _a^b A_\mu \cdot d\delta \eta ^\mu $$
$$ =-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu \color{red}{ -\left[{e\over c} A_\mu \cdot \delta \eta ^\mu \right] \Big|_a^b}+{e\over c} \int _a^b dA _\mu \cdot \delta \eta ^\mu $$
利用Thm.3同乘同除\(d\tau \)不影響變分
$$\delta S_{PF}=-{e\over c} \int _a^b \delta A_\mu \cdot d\eta ^\mu +{e\over c} \int _a^b dA _\mu \cdot \delta \eta ^\mu $$
$$ =-{e\over c} \int _a^b \delta A_\mu \cdot {d\eta ^\mu \over \color{red}{d\tau}} \color{red}{d\tau} +{e\over c} \int _a^b {dA _\mu \over \color{red}{d\tau}} \color{red}{d\tau} \cdot \delta \eta ^\mu $$
因為
$$\delta A_\mu ={\partial A_\mu \over \partial x ^\nu } \delta \eta ^\nu $$
$${dA_\mu \over d\tau} ={\partial A_\mu \over \partial x^\nu } {d\eta ^\nu \over d\tau} ={\partial A_\mu \over \partial x^\nu } U^\nu $$
代入得到
$$\delta S_{PF}=-{e\over c} \int _a^b {\partial A_\mu \over\partial x^\nu } \delta \eta ^\nu \cdot u^\mu d\tau +{e\over c} \int _a^b {\partial A_\mu \over \partial x^\nu } U^\nu d\tau \cdot \delta \eta ^\mu$$
$$=-{e\over c} \int _a^b (\partial _\nu A_\mu ) u^\mu \delta \eta ^\nu d\tau +{e\over c} \int _a^b \left(\partial _\nu A_\mu \right) U^\nu \delta \eta ^\mu d\tau $$
我們想要把變分\(\delta \eta ^\nu \)和\(\delta \eta ^\mu\) 一起提出來,但是上標不一樣。但因為每一項\(\mu\) 、\(\nu\) 都是Dummy index,可以互換\(\mu \leftrightarrow \nu\) ,我們把第一項的\(\mu\) 、\(\nu\)互換,就可以把兩項合併
$$\delta S_{PF}=-{e\over c} \int _a^b \left( \partial _{\color{red}{\mu}} A_{\color{red}{\nu}} \right) U^{\color{red}{\nu}} \delta \eta ^{\color{red}{\mu}} d\tau +{e\over c} \int _a^b (\partial _\nu A_\mu ) U^\nu \delta \eta ^\mu d\tau $$
$$=-{e\over c} \int _a^b (\partial _\mu A_\nu -\partial _\nu A_\mu ) U^\nu \delta \eta ^\mu d\tau $$
完整考慮Charge Particle在EM Field中的運動
$$\delta S=\delta S_P+\delta S_{PF}=0$$
所以
$$\delta S_P+\delta S_{PF}=\int _a^b m {dU_\mu \over d\tau} \delta \eta ^\mu d\tau -{e\over c} \int _a^b \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu \delta \eta ^\mu d\tau $$
$$=\int _a^b \left[m {dU_\mu \over d\tau} -{e\over c} \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu \right] \delta \eta ^\mu d\tau =0$$
會得到
$$m {dU_\mu \over d\tau} -{e\over c} \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu =0$$
$$m {dU_\mu \over d\tau} ={e\over c} \left(\partial _\mu A_\nu -\partial _\nu A_\mu \right) U^\nu \equiv {e\over c} F_{\mu \nu} U^\nu $$
我們定義電磁張量Electromagnetic Tensor
$$F_{\mu \nu} =\partial _\mu A_\nu -\partial _\nu A_\mu $$
電場\(\overrightarrow{E}\)、磁場\(\overrightarrow{B}\)與\(\phi\)、\(\overrightarrow{A}\)的關係(高斯制)
$$ \overrightarrow{E}=-\nabla \phi-{1\over c} {\partial \overrightarrow{A}\over \partial t}$$
$$\overrightarrow{B}=\nabla \times \overrightarrow{A} $$
其中
$$A_\nu \to \left(\phi,-A_x,-A_y,-A_z \right)$$
$$\partial _\mu \to \left({\partial \over \partial x^0},{\partial \over \partial x^1 },{\partial \over \partial x^2},{\partial \over \partial x^3 }\right)=\left({\partial \over \partial ct},{\partial \over \partial x },{\partial \over \partial y},{\partial \over \partial z }\right)$$
可以計算
$$F_{\mu \nu} =\partial _\mu A_\nu -\partial _\nu A_\mu =\left(\begin{matrix}0 & E_x & E_y & E_z\\ -E_x & 0 & -B_z & B_y \\ -E_y & B_z & 0 & -B_x \\ -E_z & -B_y & B_x & 0 \end{matrix}\right)$$
$$F^{\mu \nu} =\partial ^\mu A^\nu -\partial ^\nu A^\mu =\left(\begin{matrix}0 & -E_x & -E_y & -E_z\\ E_x & 0 & -B_z & B_y \\ E_y & B_z & 0 & -B_x \\ E_z & -B_y & B_x & 0 \end{matrix}\right)$$
 王培儒
王培儒