最小作用量原理（相對論性）

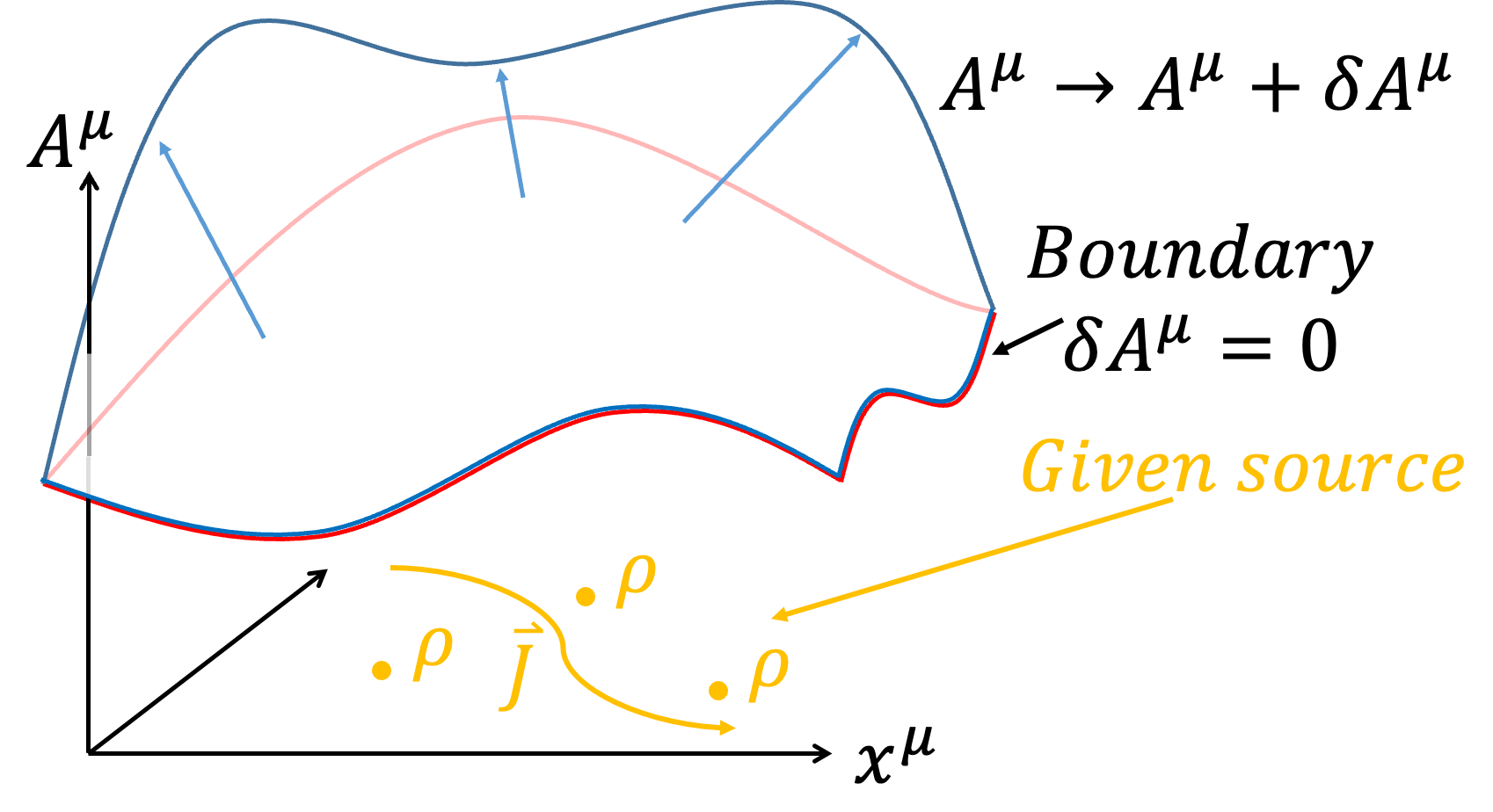
在這一部分，我們在給定Source下，討論EM Field的分佈（給定Source下表示我們不對Source下的分佈\(\eta ^\mu\) 作變分）。 $$S_{PF}+S_F=\int -\rho_m c-{1\over c^2} A_\mu J^\mu d^4 +\int-{1 \over 16\pi c} F_{\mu \nu} F^{\mu \nu} d^4 x$$ 我們想知道EM Field的分佈，所以我們針對\(A^\mu\) 作變分 $$A^\mu \to A^\mu +\delta A^\mu $$ 我們來觀察\(J^\mu \)、\(d^4 x\)、\(F^{\mu \nu}\) 會不會受到影響？

$$J^\mu =\rho_e {dx^\mu \over d\tau} =J^\mu (x^\nu )$$ $$d^4 x=d^4 x(x^\nu )$$ $$F^{\mu \nu} =\partial ^\mu A^\nu -\partial ^\nu A^\mu =F^{\mu \nu} \left(A^\omega \right)$$ 可見只有電磁張量\(F^{\mu \nu}\) 會受到\(A^\mu \)的變分\(A^\mu \to A^\mu +\delta A^\mu\) 有關 $$F^{\mu \nu} \left(A^\omega \right)\to F^{\mu \nu} (A^\omega +\delta A^\omega )=F^{\mu \nu} \left(A^\omega \right)+\delta F^{\mu \nu} $$ 所以\(S_{PF}\)的變分很簡單 $$\delta S_{PF}=\delta \int -{1 \over c^2} A_\mu J^\mu d^4 x$$ $$ =-{1 \over c^2} \int \delta A_\mu \cdot J^\mu d^4 x $$ 至於\(S_F\)的變分就稍嫌複雜 $$S_F=-{1 \over 16 \pi c} \int F_{\mu \nu} F^{\mu \nu} d^4 x$$ $$\delta S_F=-{1 \over 16 \pi c} \delta \int F_{\mu \nu} F^{\mu \nu} d^4 x =-{1 \over 16 \pi c} \int \delta F_{\mu \nu} \cdot F^{\mu \nu} +F_{\mu \nu} \cdot \delta F ^{\mu \nu} d^4 x $$ 利用Thm.4: 對Scalar變分與上下標無關，所以\(\delta F_{\mu \nu} \cdot F^{\mu \nu} =F_{\mu \nu} \cdot \delta F ^{\mu \nu}\) ，會有兩倍 $$\delta S_F=-{1 \over 16 \pi c} \int 2\delta F_{\mu \nu} \cdot F^{\mu \nu} d^4 x =-{1 \over 8 \pi c} \int \delta F_{\mu \nu} \cdot F^{\mu \nu} d^4 x $$ $$=-{1 \over 8 \pi c} \int \delta (\partial _\mu A_\nu -\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ $$=-{1 \over 8 \pi c} \int \delta (\partial _\mu A_\nu )\cdot F^{\mu \nu} d^4 x +{1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ 因為每一項\(\mu\) 、\(\nu\) 都是Dummy index，可以互換\(\mu \leftrightarrow \nu \)，我們把第一項的\(\mu\) 、\(\nu\) 互換，就可以把兩項合併 $$\delta S_F=-{1 \over 8 \pi c} \int \delta (\partial _{\color{red}{\nu}} A_{\color{red}{\mu}} )\cdot F^{\color{red}{\nu \mu}} d^4 x +{1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ $$={1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot (-F^\nu \mu +F^{\mu \nu} ) d^4 x $$ 回憶電磁張量 $$F^{\mu \nu} =\partial ^\mu A^\nu -\partial ^\nu A^\mu =\left(\begin{matrix}0 & -E_x & -E_y & -E_z\\ E_x & 0 & -B_z & B_y \\ E_y & B_z & 0 & -B_x \\ E_z & -B_y & B_x & 0 \end{matrix}\right)$$ \(F^{\mu \nu} \)是一個反對稱張量，所以\(F^\nu \mu =-F^{\mu \nu} \) 代回去會多兩倍 $$\delta S_F={1 \over 8 \pi c} \int \delta (\partial _\nu A_\mu )\cdot (F^{\color{red}{\mu \nu}} +F^{\mu \nu} ) d^4 x ={1 \over 4 \pi c} \int \delta (\partial _\nu A_\mu )\cdot F^{\mu \nu} d^4 x $$ 利用Thm.1的方法，我們將\(\delta\) 和\(\partial _\nu \)對調 $$\delta (\partial _\nu A_\mu )=\partial _\nu (\delta A_\mu )$$ $$\delta S_F={1 \over 4 \pi c} \int \partial _\nu (\delta A_\mu )\cdot F^{\mu \nu} d^4 x $$ 利用微分的Chain rule， $$\partial _\nu (\delta A_\mu )\cdot F^{\mu \nu} =\partial _\nu (\delta A_\mu \cdot F^{\mu \nu} )-\delta A_\mu \cdot \partial _\nu (F^{\mu \nu} )$$ 將積分拆成兩項 $$\delta S_F={1 \over 4 \pi c} \int \partial _\nu (\delta A_\mu \cdot F^{\mu \nu} ) d^4 x -{1 \over 4 \pi c} \int \delta A_\mu \cdot \partial _\nu (F^{\mu \nu} ) d^4 x $$

回憶Divergence theorem $$\int \nabla \cdot \overrightarrow{F}dV =∮ \overrightarrow{F}\cdot d\overrightarrow{S} $$ 一個體積分，可以改寫成對體表面的面積分。寫成Levi-Civita symbol $$\int \partial _\nu F^\nu dV =∮ F^\nu dS_\nu $$

所以第一項利用Divergence theorem，但是Boundary上的\(\delta A_\mu =0\)，所以 $${1 \over 4 \pi c} \int \partial _\nu (\delta A_\mu \cdot F^{\mu \nu} ) d^4 x ={1 \over 4 \pi c} ∮ \delta A_\mu \cdot F^{\mu \nu} dS_\nu =0$$ 所以 $$\delta S_F=-{1 \over 4 \pi c} \int \partial _\nu (F^{\mu \nu} )\cdot \delta A_\mu d^4 x $$ 合併\(\delta S_{PF}+\delta S_F\) $$\delta S_{PF}+\delta S_F=-{1 \over c^2} \int J^\mu \cdot \delta A_\mu d^4 x -{1 \over 4 \pi c} \int \partial _\nu (F^{\mu \nu} )\cdot \delta A_\mu d^4 x$$ $$=\int \left[-{1 \over c^2} J^\mu -{1 \over 4 \pi c} \partial _\nu F^{\mu \nu} \right]\delta A_\mu d^4 x =0$$ 會得到 $$-{1 \over c^2} J^\mu -{1 \over 4 \pi c} \partial _\nu F^{\mu \nu} =0$$ $$\partial _\nu F^{\mu \nu} =-{4\pi \over c} J^\mu $$

Recall Maxwell's equation in Gaussian Unit $$ \nabla \cdot \overrightarrow{E}=4\pi \rho_e$$ $$ \nabla \cdot \overrightarrow{B}=0)$$ $$ \nabla ×\overrightarrow{E}=-{1 \over c} {\partial \overrightarrow{B} \over \partial t}$$ $$ \nabla ×\overrightarrow{B}={4\pi \over c} \overrightarrow{J}+{1 \over c} {\partial \overrightarrow{E} \over \partial t }$$

$$\partial _\nu F^{\mu \nu} =-{4\pi \over c} J^\mu \to \left( \begin{matrix} \nabla \cdot \overrightarrow{E}=4\pi \rho_e \\ \nabla ×\overrightarrow{B}={4\pi \over c} \overrightarrow{J}+{1 \over c} {\partial \overrightarrow{E}\over \partial t} \end{matrix}\right)$$

$$F_{\mu \nu} =\partial _\mu A_\nu -\partial _\nu A_\mu $$ 電磁張量有特別的關係式(Bianchi identity) $$\partial _\omega F_{\mu \nu} +\partial _\mu F_{\nu \omega} +\partial _\nu F_{\omega \mu} =\partial _{[\omega} F_{\mu \nu ]} =0$$ 展開 $$\partial _\omega (\partial _\mu A_\nu -\partial _\nu A_\mu )+\partial _\mu (\partial _\nu A_\omega -\partial _\omega A_\nu )+\partial _\nu (\partial _\omega A_\mu -\partial _\mu A_\omega )=0$$ $$\partial _\omega \partial _\mu A_\nu -\partial _\omega \partial _\nu A_\mu +\partial _\mu \partial _\nu A_\omega -\partial _\mu \partial _\omega A_\nu +\partial _\nu \partial _\omega A_\mu -\partial _\nu \partial _\mu A_\omega =0$$ 這條關係式會得到

$$ \partial _\omega F_{\mu \nu} +\partial _\mu F_\nu \omega +\partial _\nu F_\omega \mu =0 \to \left( \begin{matrix} \nabla \cdot \overrightarrow{B}=0 \\ \nabla ×\overrightarrow{E}=-{1 \over c} {\partial \overrightarrow{B} \over \partial t} \end{matrix}\right)$$