連續場與波動方程
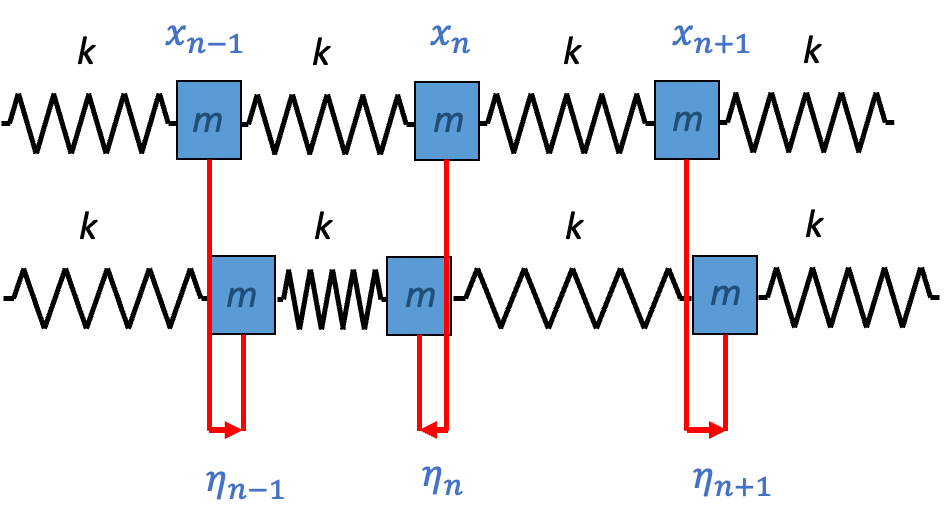
從單質點進入到連續場之中,物理學家是利用串聯無窮多的簡諧振子去描述一個連續場。針對無窮多的簡諧振子,可以寫下Lagrangian
$$\mathcal{L}=∑_n^∞ {1 \over 2} m\eta ̇_n-{1 \over 2} k(\eta _n-\eta _(n-1) )^2 $$
其中\eta _n是位置n的振幅,\eta ̇_n是位置n的振盪的速度。

進入到連續場時,Lagrangian為
$$\mathcal{L}=\int {1 \over 2} \rho\left({\partial \eta \over\partial t}\right)^2-{1 \over 2} Y\left({\partial \eta \over\partial x}\right)^2 dx $$
其中\(\rho\)為質量密度、\(Y\)為楊氏係數。

在三維Lagrangian為
$$\mathcal{L}=\int {1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2 dV$$
可以直接看出Lagrangian dendity \(\mathcal{L}={1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2\)。一樣的,我們可以利用Variational principle得到連續場的運動方程。作用量Action為
$$S=\int Ld^4 x =\int {1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2 d^4 x $$
將場振幅做變分 \(\eta (x^\mu )\to \eta (x^\mu )+\delta \eta (x^\mu )\),Action變化要為極值:
$$\delta S=\delta \int {1 \over 2} \rho(\partial _t \eta )^2-{1 \over 2} Y( \nabla \eta )^2 d^4 x $$
$$=\int \rho\partial _t \eta *\delta (\partial _t \eta )-Y \nabla \eta *\delta ( \nabla \eta ) d^4 x $$
將變分和微分交換
$$=\int \rho\partial _t \eta \partial _t (\delta \eta )-Y \nabla \eta \nabla (\delta \eta ) d^4 x $$
$$=\int \rho\partial _t \eta \partial _t (\delta \eta ) d^4 x -\int Y \nabla \eta \nabla (\delta \eta ) d^4 x $$
$$=\int \partial _t (\rho\partial _t \eta \delta \eta ) d^4 x -\int \partial _t (\rho\partial _t \eta )*\delta \eta d^4 x -\int \nabla (Y \nabla \eta \delta \eta ) d^4 x +\int \nabla (Y\eta )*\delta \eta d^4 x $$
$$=\left[-\int \partial _t (\rho\partial _t \eta )*\delta \eta d^4 x +\int \nabla (Y\eta )*\delta \eta d^4 x \right]+\left[\int \partial _t (\rho\partial _t \eta \delta \eta ) d^4 x -\int \nabla (Y \nabla \eta \delta \eta ) d^4 x \right]$$
後面為邊界項,利用Integral by part
$$=-\int \left[\rho\partial _t^2 \eta -Y \nabla ^2 \eta \right]*\delta \eta d^4 x +\left[\int \rho\partial _t \eta \delta \eta d^3 x \Big|_{t_1}^{t_2}- \int Y \nabla \eta \delta \eta d^3 x \Big|_{\partial x,\partial y,\partial z} \right]$$
$$=-\int [\rho\partial _t^2 \eta -Y \nabla ^2 \eta ]*\delta \eta d^4 x +0$$
因為\(\delta \eta\) 為任意,得到
$$\rho\partial _t^2 \eta -Y \nabla ^2 \eta =0$$
$$ \nabla ^2 \eta ={\rho \over Y} \partial _t^2 \eta $$
令\(v=\sqrt{{Y\over \rho}}\)
$$\nabla ^2 \eta ={1\over v^2} \partial _t^2 \eta $$
即波動方程。
 王培儒
王培儒